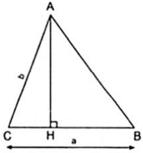
Xét tam giác ABC có BC = a, AC = b
Kẻ AH ⊥ BC thì AH và AC lần lượt là đường xiên.
Đường vuông góc kẻ từ A ở ngoài đường thẳng BC đến đường thẳng đó nên đường AH là đường ngắn nhất hay AH ≤ AC.
Khi đó ta có: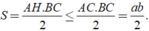
Mặt khác ta có:
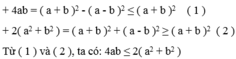
⇒ 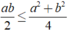
hay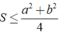 (đpcm)
(đpcm)

Xét tam giác ABC có BC = a, AC = b
Kẻ AH ⊥ BC thì AH và AC lần lượt là đường xiên.
Đường vuông góc kẻ từ A ở ngoài đường thẳng BC đến đường thẳng đó nên đường AH là đường ngắn nhất hay AH ≤ AC.
Khi đó ta có: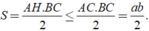
Mặt khác ta có:
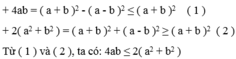
⇒ 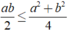
hay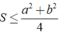 (đpcm)
(đpcm)
Chứng minh rằng : a) S \(\le\frac{a^2+b^2}{4}\)với S là diện tích của tam giác có độ dài hai cạnh bằng a , b .
Chứng minh:
a) S \(\le\) \(\frac{a^2+b^2}{4}\)với S là diện tích tam giác có độ dài 2 cạnh bằng a,b
b) S \(\le\) \(\frac{a^2+b^2+c^2+d^2}{4}\)với S là diện tích tứ giác có độ dài 4 cạnh bằng a, b, c, d
Cho S là diện tích của tứ giác ABCD có độ dài các cạnh là a, b, c, d. Chứng minh S ≤ (a^2 + b^2 + c^2 + d^2)/4
Cho a, b, c là độ dài các cạnh của một tam giác, S là diện tích, p là nửa chu vi tam giác đó. Chứng minh rằng:
a4 + b4 + c4 >= 16S2
1, Áp dụng định lý Pytago. Chứng minh rằng nếu ta có a, b, c > 0 sao cho a = m2 + n2 ; b = m2 - n2 ; c = 2mn thì a, b, c là số đo 3 cạnh của tam giác vuông.
2, Các ạnh góc vuông của một tam giác vuông có độ dài a, b và diện tích bằng S. Tính các góc của tam giác vuông đó biết (a + b)2
3, Chứng minh rằng nếu a, b, c là độ dài ba cạnh của 1 tam giác vuông (với a là độ dài cạnh huyền) thì các số x, y, z sau đây cũng là độ dài cạnh của tam giác vuông: x = 9a + 4b +8c ; y = 4a + b+ 4c ; z = 8a + 4b + 7c
gọi S là diện tích tứ giác ABCD có độ dài các cạnh là a,b,c,d .
Chứng minh rằng : S ≤( a2+b2+c2+d2 )/4
cho tam giác ABC có độ dài 3 cạnh bằng a,b,c, diện tích bằng S. Chứng minh rằng 6S<=a^2+b^2+c^2
1. Các cạnh góc vuông của tam giác vuông có độ dài là a, b và diện tích bằng S. Tìm các góc của tam giác vuông biết (a+b)2 = 8S
2. Cho tam giác ABC với trung tuyến CM. Điểm D thuộc đoạn BM sao cho BD=2MD. Biết rằng góc MCD bằng góc BCD. Chứng minh rằng góc ACD bằng 900
GÍUP MÌNH Với!!
1. Tính diện tích một hình thang vuông, biết hai đáy có độ dài 6cm và 9cm, góc tạo bởi cạnh bên và đáy lớn có số đo bằng 45o
2. Cho hình thang ABCD có độ dài hai đáy AB = 5cm, CD = 15cm, độ dài hai đường chéo AC = 16cm, BD = 12cm. Từ A vẽ đường thẳng song song với BD, cắt CD tại E
a) Chứng minh tam giác ACE là tam giác vuông
b) Tính diện tích hình thang ABCD
3. Gọi O là điểm nằm trong hình bình hành ABCD . Chứng minh: SABO + SCDO = SBCO + SDAO