Cho đường thẳng (d) có phương trình: x- 2y+ 5= 0. Có mấy phương trình đường thẳng qua M(2; 1) và tạo với d một góc 450.
A. 1
B. 2
C. 3
D. Không có.
Cho đường thẳng (d) có phương trình 4x+3y-5=0 và đường thẳng ( ∆ ) có phương trình x+2y-5=0 Phương trình đường thẳng (d') là ảnh của (d) qua phép đối xứng trục ( ∆ ) là:
A. x-3=0
B. x+y-1=0
C. 3x+2y-5=0
D. y-3=0
Đường thẳng (d) có phương trình 4x+3y-5=0 và đường thẳng có phương trình x+2y-5=0. Phương trình đường thẳng d’ là ảnh của đường thẳng d qua phép đối xứng trục △ là
![]()
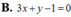
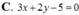
![]()
Trong mặt phẳng Oxy cho đường thẳng d có phương trình 3x − 2y – 6 = 0
a) Viết phương trình của đường thẳng d 1 là ảnh của d qua phép đối xứng qua trục Oy
b) Viết phương trình của đường thẳng d 2 là ảnh của d qua phép đối xứng qua đường thẳng Δ có phương trình x + y – 2 = 0 .
a) d 1 : 3x + 2y + 6 = 0
b) Giao của d và Δ là A(2;0). Lấy B(0; −3) thuộc d. Ảnh của B qua phép đối xứng của đường thẳng Δ là B′(5;2). Khi đó d' chính là đường thẳng AB′: 2x − 3y – 4 = 0
Cho đường thẳng (d) có phương trình 4 x + 3 y − 5 = 0 và đường thẳng ∆ có phương trình x + 2 y − 5 = 0. Phương trình đường thẳng (d') là ảnh của (d) qua phép đối xứng trục ∆ là:
A. x − 3 = 0
B. x + y − 1 = 0
C. 3 x + 2 y − 5 = 0
D. y − 3 = 0
Cho đường thẳng (d) x-2y+ 8= 0. Đường thẳng ∆ đi qua A(2; -3) và song song với (d) có phương trình:
A. x- 2y+ 6= 0
B. 2x+ y -1= 0
C.x+ 2y-6= 0
D.x-2y-8=0
Đáp án D
Do ∆ song song vớo ( d) nên có phương trình dạng: x- 2y+ c= 0
Mà ∆ đi qua A( 2; -3) nên ta có
2- 2. (-3) + c= 0
Do đó: c= - 8.
Vậy đường thẳng cần tìm là x- 2y – 8 = 0
cho đường thẳng (d) : x - 2y + 1 = 0. nếu đường thẳng (Δ) đi qua M(1;-1) và song song với (d) thì (Δ) có phương trình ?
\(\Delta\) đi qua M(1,-1) có hệ số góc k
=> \(\Delta:y=k\left(x-1\right)-1=kx-k-1\)
\(\Delta\) song song d: \(y=\dfrac{1}{2}x+\dfrac{1}{2}\) \(=>k=\dfrac{1}{2}\)
\(\Delta:y=\dfrac{1}{2}x-\dfrac{3}{2}\)
Trong mặt phẳng tọa độ Oxy cho đường thằng d có phương trình 2y+x+3=0. Phương trình đường thẳng d’ là ảnh của đường thẳng d qua phép đối xứng trục Ox là
A. y-2x+3=0.
B. -2y+x+3=0.
C. 2y+x-3=0.
D. 2y-x+3=0.
Trong mặt phẳng Oxy cho đường thẳng d có phương trình 3x - 2y - 1 = 0. ảnh của đường thẳng d qua phép đối xứng tâm O có phương trình là:
A. 3x + 2y + 1 = 0
B. -3x + 2y -1 = 0
C. 3x + 2y - 1 = 0
D. 3x - 2y - 1 = 0
Qua phép đối xứng tâm O biến điểm M(x; y) thuộc đường thẳng d thẳng điểm M’ (x’; y’) thuộc đường thẳng d’.
Ta có: x ' = − x y ' = − y ⇔ x = − x ' y = − y '
Vì điểm M thuộc d nên: 3x – 2y – 1 = 0
Suy ra: 3. (-x’) – 2(- y’) -1 = 0 hay - 3x’ + 2y’ – 1=0
Vây phương trình đường thẳng d’ là - 3x + 2y - 1= 0
Đáp án B
Trong mặt phẳng tọa độ Oxy, cho điểm M(3; -5), đường thẳng d có phương trình 3x + 2y – 6 = 0 và đường tròn (C) có phương trình x 2 + y 2 − 2 x + 4 y – 4 = 0 . Tìm ảnh của M, d, và (C) qua phép đối xứng qua trục Ox
Gọi M′, d′ và (C') theo thứ tự là ảnh của M, d và (C) qua phép đối xứng qua trục Ox .
Khi đó M′ = (3;5) . Để tìm ta viết biểu thức tọa độ của phép đối xứng qua trục:
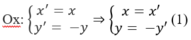
Thay (1) vào phương trình của đường thẳng d ta được 3x′ − 2y′ − 6 = 0.
Từ đó suy ra phương trình của d' là 3x − 2y – 6 = 0
Thay (1) vào phương trình của (C) ta được x ' 2 + y ' 2 − 2 x ′ + 4 y ′ − 4 = 0 .
Từ đó suy ra phương trình của (C') là x − 1 2 + y − 2 2 = 9 .
Cũng có thể nhận xét (C) có tâm là I(1; −2), bán kính bằng 3,
từ đó suy ra tâm I' của (C') có tọa độ (1;2) và phương trình của (C') là x − 1 2 + y − 2 2 = 9