Giải các phương trình 124 – 4x = 0.

Những câu hỏi liên quan
giải các phương trình sau 1, 2x² - 5x + 1 = 0 2, 4x² + 4x + 1 = 0
pt 1:
\(\Delta=\left(-5\right)^2-4.2.1=25-8=16\)
=> pt có 2 nghiệm
\(x=\dfrac{-\left(-5\right)+\sqrt{16}}{2.2}=\dfrac{9}{4}\)
\(x=\dfrac{-\left(-5\right)-\sqrt{16}}{2.2}=\dfrac{1}{4}\)
pt 2:
\(\Leftrightarrow\left(2x+1\right)^2=0\)
\(\Leftrightarrow x=-\dfrac{1}{2}\)
Đúng 2
Bình luận (1)
Giải các phương trình sau 2x+6=0 3x-9=0 4x+20=0 4x+1=6-x
\(\text{ 2x+6=0 }\)
\(\Leftrightarrow2x=-6\)
\(\Leftrightarrow x=-3\)
\(S=\left\{-3\right\}\)
\(\text{3x-9=0 }\)
\(\Leftrightarrow3x=9\)
\(\Leftrightarrow x=3\)
\(S=\left\{3\right\}\)
\(\text{4x+20=0}\)
\(\Leftrightarrow4x=-20\)
\(\Leftrightarrow x=-5\)
\(S=\left\{-5\right\}\)
\(\text{4x+1=6-x}\)
\(\Leftrightarrow4x+1-6-x=0\)
\(\Leftrightarrow3x-5=0\)
\(\Leftrightarrow3x=5\)
\(\Leftrightarrow x=\dfrac{5}{3}\)
\(S=\left\{\dfrac{5}{3}\right\}\)
Đúng 1
Bình luận (0)
a: 2x+6=0
=>2x=-6
=>x=-3
b: 3x-9=0
=>3x=9
=>x=3
c: 4x+20=0
=>x+5=0
=>x=-5
d: 4x+1=6-x
=>5x=5
=>x=1
Đúng 0
Bình luận (0)
\(4x+1=6-x\)
\(\Leftrightarrow4x+1-6+x=0\)
\(\Leftrightarrow5x-5=0\)
\(\Leftrightarrow5x=5\)
\(\Leftrightarrow x=1\)
\(S=\left\{1\right\}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giải các phương trình sau 4x-4,5 =0
Giải các phương trình sau bằng cách đưa về phương trình tích 3 x 3 +6 x 2 -4x =0
Ta có: 3 x 3 +6 x 2 -4x =0 ⇔ x(3 x 2 +6x -4) =0
⇔ x = 0 hoặc 3 x 2 +6x -4 =0
Giải phương trình 3 x 2 +6x -4 =0
∆ ’ = 3 2 - 3(-4) = 9 + 12 = 21 > 0
∆ ' = 21
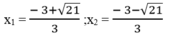
Vậy phương trình đã cho có 3 nghiệm
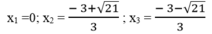
Đúng 0
Bình luận (0)
Giải các phương trình sau: 4x - x - 18 = 0
Ta có: 4x - x - 18 = 0 ⇔ 3x - 18 = 0 ⇔ 3x = 18 ⇔ x = 18/3 = 6.
Vậy phương trình có nghiệm là x = 6.
Đúng 0
Bình luận (0)
Giải các phương trình sau: (4x – 10)(24 + 5x) = 0
(4x – 10)(24 + 5x) = 0 ⇔ 4x – 10 = 0 hoặc 24 + 5x = 0
4x – 10 = 0 ⇔ 4x = 10 ⇔ x = 2,5
24 + 5x = 0 ⇔ 5x = -24 ⇔ x = -4,8
Phương trình có nghiệm x = 2,5 và x = -4,8
Đúng 0
Bình luận (0)
Giải các phương trình sau: ( 4 x - 10 ) ( x 2 + 2 ) = 0
Giải các phương trình sau: ( 5x - 4 )( 4x + 6 ) = 0
Ta có: ( 5x - 4 )( 4x + 6 ) = 0
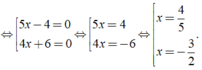
Vậy phương trình đã cho có tập nghiệm là S = { - 3/2; 4/5 }.
Đúng 0
Bình luận (0)
bài 1 : Giải các phương trình sau: a/ 4x + 20 = 0
b/ 2x – 3 = 3(x – 1) + x + 2
bài 2 : Giải các phương trình sau: a/ (3x – 2)(4x + 5) = 0
b/ 2x(x – 3) – 5(x – 3) = 0
a/ 4x + 20 = 0
⇔4x = -20
⇔x = -5
Vậy phương trình có tập nghiệm S = {-5}
b/ 2x – 3 = 3(x – 1) + x + 2
⇔ 2x-3 = 3x -3+x+2
⇔2x – 3x = -3+2+3
⇔-2x = 2
⇔x = -1
Vậy phương trình có tập nghiệm S = {-1}
Đúng 0
Bình luận (0)
câu tiếp theo
a/ (3x – 2)(4x + 5) = 0
3x – 2 = 0 hoặc 4x + 5 = 0
3x – 2 = 0 => x = 3/24x + 5 = 0 => x = – 5/4Vậy phương trình có tập nghiệm S= {-5/4,3/2}
b/ 2x(x – 3) – 5(x – 3) = 0
=> (x – 3)(2x -5) = 0
=> x – 3 = 0 hoặc 2x – 5 = 0
* x – 3 = 0 => x = 3
* 2x – 5 = 0 => x = 5/2
Vậy phương trình có tập nghiệm S = {0, 5/2}
Đúng 0
Bình luận (0)
b1
a. 4x+ 20=0 <=> 4x= -20 <=> x= -20/4 <=> x= -5
b. 2x- 3= 3(x- 1)+ x+ 2 <=> 2x- 3= 3x- 3+ x+ 2
<=> 2x- 3= 4x- 1 <=> 2x- 4x= -1+ 3 <=> -2x= 2
<=> x= 2/-2 <=> x= -1
b2
a. (3x- 2)(4x+ 5)= 0
<=>\(\orbr{\begin{cases}3x-2=0\\4x+5=0\end{cases}\Leftrightarrow\orbr{\begin{cases}3x=2\\4x=-5\end{cases}}}\)
<=>\(\orbr{\begin{cases}x=\frac{2}{3}\\x=-\frac{5}{4}\end{cases}}\)
b. 2x(x- 3)- 5(x- 3)= 0
<=> (x- 3)(2x- 5)= 0
<=> \(\orbr{\begin{cases}x-3=0\\2x-5=0\end{cases}\Leftrightarrow}\orbr{\begin{cases}x=3\\2x=5\end{cases}}\)
<=> \(\orbr{\begin{cases}x=3\\x=\frac{5}{2}\end{cases}}\)
Đúng 0
Bình luận (0)