Cho x O y ^ và y O z ^ là hai góc kề nhau, biết x O y ^ = 70 0 , y O z ^ = 60 0 . Tính x O z ^ ?

Những câu hỏi liên quan
Cho góc xOz kề bù góc y o z biết rằng góc x O y- góc y o z = 20 độ Tính góc xOy và góc yOz
Cho hai góc nhọn xOy và x'O'y' có các cạnh tương ứng Ox // O'x' , Oy // O'y'. Vẽ các tia Oz và O'z' lần lượt là phân giác của góc xOy và x'O'y'. Chứng tỏ :
a) Hai góc xOy và x'O'y' bằng nhau.
b) Oz // O'z'.
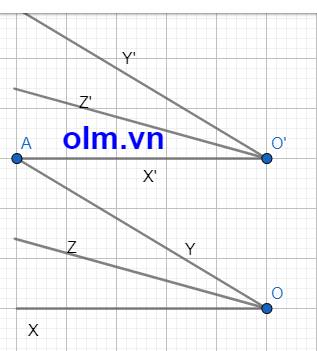
a,Kéo dài OY cắt O'X' tại A ta có:
\(\widehat{XOY}\) = \(\widehat{XOA}\) = \(\widehat{OAO'}\) (so le trong) (1)
\(\widehat{Y'O'X'}\) = \(\widehat{Y'O'A}\) = \(\widehat{OAO'}\) (so le trong) (2)
Kết hợp (1) Và (2) ta có:
\(\widehat{XOY=}\) \(\widehat{X'O'Y'}\) (đpcm)
Đúng 0
Bình luận (0)
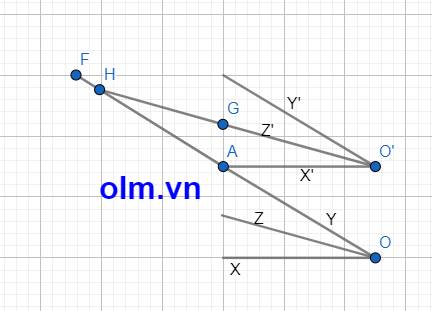
b, Kéo dài OY cắt O'Z' tại H
\(\widehat{ZOA}\) = \(\dfrac{1}{2}\) \(\widehat{XOY}\) (vì OZ là phân giác của góc XOY
\(\widehat{HO'A}\) = \(\dfrac{1}{2}\) \(\widehat{X'O'Y'}\) (vì OY là phân giác của góc X'O'Y')
Mặt khác ta có \(\widehat{OAO'}\) = \(\widehat{HO'A}\) + \(\widehat{AHO'}\) (góc ngoài tam giác bằng tổng hai góc trong không kề với nó)
\(\widehat{HO'A}\) = \(\dfrac{1}{2}\) \(\widehat{OAO'}\) ⇒ \(\widehat{AHO'}\) = \(\dfrac{1}{2}\) \(\widehat{OAO'}\) = \(\dfrac{1}{2}\) \(\widehat{XOY}\)
⇒ \(\widehat{ZOA}\) = \(\widehat{AHO'}\) (hai góc này ở vị trí so le trong)
⇒ OZ // O'Z' (đpcm)
Đúng 0
Bình luận (0)
Cho x,y,z là 3 số khác 0 và x+y+z=o. Tính giá trị của biểu thức:
xy/x^2+y^2-z^2 + xz/x^2+z^2-y^2 + yz/y^2+z^2-x^2
Giúp mình với, tks!!
Ta có: \(x^2+y^2-z^2\)
\(=\left(x+y\right)^2-z^2-2xy\)
\(=\left(x+y+z\right)\left(x+y-z\right)-2xy\)
\(=-2xy\)
Ta có: \(x^2+z^2-y^2\)
\(=\left(x+z\right)^2-y^2-2xz\)
\(=\left(x+y+z\right)\left(x+z-y\right)-2xz\)
\(=-2xz\)
Ta có: \(y^2+z^2-x^2\)
\(=\left(y+z\right)^2-x^2-2yz\)
\(=\left(x+y+z\right)\left(y+z-x\right)-2yz\)
\(=-2yz\)
Ta có: \(\dfrac{xy}{x^2+y^2-z^2}+\dfrac{xz}{x^2+z^2-y^2}+\dfrac{yz}{y^2+z^2-x^2}\)
\(=\dfrac{xy}{-2xy}+\dfrac{xz}{-2xz}+\dfrac{yz}{-2yz}\)
\(=\dfrac{1}{-2}+\dfrac{1}{-2}+\dfrac{1}{-2}\)
\(=\dfrac{-3}{2}\)
Đúng 1
Bình luận (0)
Cho x,y,z khác o và x-y-z=0.
Tính giá trị biểu thức: \(A=\left(1-\frac{z}{x}\right).\left(1-\frac{x}{y}\right).\left(1+\frac{y}{z}\right)\)
Ta có: x - y - z = 0 \(\Rightarrow\begin{cases}x-z=y\\y-x=-z\\z+y=x\end{cases}\)
\(A=\left(1-\frac{z}{x}\right).\left(1-\frac{x}{y}\right).\left(1+\frac{y}{z}\right)\)
\(A=\frac{x-z}{x}.\frac{y-x}{y}.\frac{z+y}{z}\)
\(A=\frac{y}{x}.\frac{-z}{y}.\frac{x}{z}=-1\)
Đúng 0
Bình luận (0)
cho biểu thức P=X/x+y+Y/y+z+Z/z+x với x,y,z là số >o
Tìm các số x,y,zkhacs o biết x^2*y*z=-4;x*y^2*z=2 và x*y*z^2=-2
(x^2*y*z) * (x*y^2*z) * (x*y*z^2)=-4*2*(-2)
=>(x*y*z)^4=16
=>x*y*z=2, mà x^2*x*y=-4=>x=-4/2=-2
TT: y=1,z=-1
Vậy x=-2;y=1;z=-1
Đúng 0
Bình luận (0)
cho x,y,z là các số thực thỏa mãn -1<=x,y,z <=1 và x+y+z =o. tìm GTNN biểu thức :P=căn bậc 2 1+x+y^2 +căn bậc 2 của 1+y+z^2 + căn bậc 2 của 1+z+x^2
Cho các góc sau: \widehat{xOy}=44^o;\quad\widehat{yOz}=52^oxOy=44o;yOz=52o. Hỏi số đo góc \widehat{xOz}xOz phải có số đo bằng bao nhiêu để tia OyOy nằm giữa hai tia OxOx và OzOz?
Khi cho hai chất X và Y trùng ngưng tạo ra polime Z có công thức
-
O
-
C
H
2
-
C
H
2
-
O
-
C
O...
Đọc tiếp
Khi cho hai chất X và Y trùng ngưng tạo ra polime Z có công thức
- O - C H 2 - C H 2 - O - C O ∥ - C 6 H 4 - C O ∥ - n
Công thức của X, Y lần lượt là
A. HO-CH2-CH2-OH; HOOC-C6H4-COOH.
B. HO-CH2-COOH; HO-C6H4-COOH.
C. HOOC-CH2CH2-COOH; HO-C6H4-OH.
D. cả A, B, C đều đúng.
Câu 11: Biết x o ; y o ; z o là nghiệm nguyên dương của phương trình x 2 + y 2 + z 2 = xy + 3y + 2x
- 4. Khi đó x o + y o + z o = .....



















