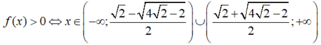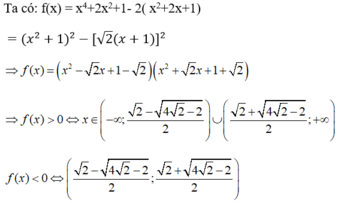Xét dấu biểu thức sau: f ( x ) = 2 x + 1 x - 1 x + 2

Những câu hỏi liên quan
Xét dấu của biểu thức sau :
f(x) = (1+x)(x-2)^2(4-x)
Xem chi tiết
Xét f(x) = (1+x)(x-2)2(4-x)
f(x) = 0 \(\Leftrightarrow\) x = -1 hoặc x = 2 hoặc x = 4
ta có bảng
x \(-\infty\) -1 2 4 \(+\infty\)
1+x - 0 + | + | +
(x-2)2 + | + 0 + | +
4-x + | + | + 0 -
f(x) - 0 + 0 + 0 -
Chúc bn học tốt
Đúng 1
Bình luận (0)
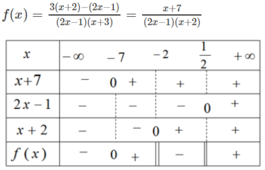
Xét dấu biểu thức sau: f ( x ) = 3 2 x - 1 - 1 x + 2
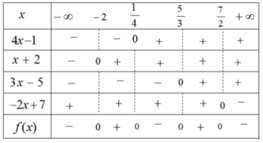
Xét dấu biểu thức sau: f(x) = (4x - 1)(x + 2)(3x - 5)(-2x + 7)
Bài 3: Xét dấu các biểu thức sau 1/ f(x) = (2x - 1)(x ^ 3 - 1)
. 2 / (f(x)) = (- 2x ^ 2 + 7x + 7)/(x ^ 2 - 3x - 10) - 1
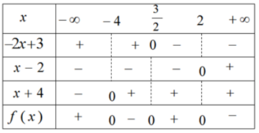
Xét dấu biểu thức sau: f(x) = (-2x + 3)(x - 2)(x + 4)
Xét dấu biểu thức sau đây:\(f\left(x\right)=\) \(\dfrac{2x+3}{x+1}+\dfrac{x+6}{-3x-2}\)
Xét dấu của các biểu thức sau : f(x) ( -x2+x-1)(6x2-5x+1) A. f(x) 0 khi và chỉ khi
x
∈
1
3
;
1
2
B. f(x) 0 khi và chỉ khi
x
∈
1
3
;...
Đọc tiếp
Xét dấu của các biểu thức sau :
f(x) = ( -x2+x-1)(6x2-5x+1)
A. f(x) > 0 khi và chỉ khi x ∈ 1 3 ; 1 2
B. f(x) < 0 khi và chỉ khi x ∈ 1 3 ; 1 2
C. f(x)>0 khi và chỉ khi x ∈ - ∞ ; 1 3 ∪ 1 2 ; + ∞
D. f(x)< 0 khi và chỉ khi x ∈ - ∞ ; 1 3
Chọn A
Ta có –x2+x-1= 0 vô nghiệm,
6x2- 5x+1= 0 khi x= ½ hoặc x= 1/3
Bảng xét dấu
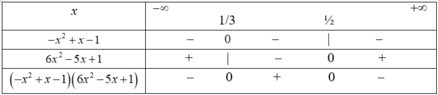
Suy ra f(x) > 0 khi và chỉ khi 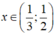
Và f( x)< 0 khi và chỉ khi 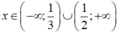
Đúng 0
Bình luận (0)
Lập bảng xét dấu biểu thức sau: f(x) = (3x2 - 4x)(2x2 - x - 1)
f(x) = (3x2 – 4x)(2x2 – x – 1)
+ Tam thức 3x2 – 4x có hai nghiệm x = 0 và x = 4/3, hệ số a = 3 > 0.
Do đó 3x2 – 4x mang dấu + khi x < 0 hoặc x > 4/3 và mang dấu – khi 0 < x < 4/3.
+ Tam thức 2x2 – x – 1 có hai nghiệm x = –1/2 và x = 1, hệ số a = 2 > 0
Do đó 2x2 – x – 1 mang dấu + khi x < –1/2 hoặc x > 1 và mang dấu – khi –1/2 < x < 1.
Ta có bảng xét dấu:
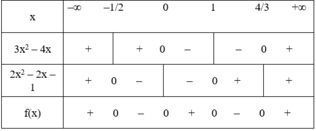
Kết luận:
f(x) > 0 ⇔ x ∈ (–∞; –1/2) ∪ (0; 1) ∪ (4/3; +∞)
f(x) = 0 ⇔ x ∈ {–1/2; 0; 1; 4/3}
f(x) < 0 ⇔ x ∈ (–1/2; 0) ∪ (1; 4/3)
Đúng 0
Bình luận (0)
Xét dấu của biểu thức sau : f(x) x4 – 4x + 1 A. B. C. D.
Đọc tiếp
Xét dấu của biểu thức sau : f(x) = x4 – 4x + 1
A. 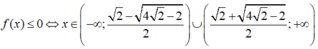
B. 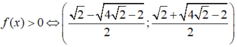
C. 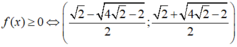
D.