Cho đường thẳng ∆ có phương trình x = − 2 + 5 t y = 3 − 2 t Vectơ nào sau đây là vectơ chỉ phương của ∆?
A. u 1 → = − 2 ; 3
B. u 2 → = 2 ; 3
C. u 3 → = 5 ; 2
D. u 4 → = − 10 ; 4
Những câu hỏi liên quan
Cho đường thẳng (d) có phương trình
4
x
+
3
y
−
5
0
và đường thẳng
∆
có phương trình
x
+
2
y
−
5
0.
Phương trình đường thẳng (d) là ảnh của (d) qua phép đối xứng trục
∆
là: A.
x
−
3
0
B. ...
Đọc tiếp
Cho đường thẳng (d) có phương trình 4 x + 3 y − 5 = 0 và đường thẳng ∆ có phương trình x + 2 y − 5 = 0. Phương trình đường thẳng (d') là ảnh của (d) qua phép đối xứng trục ∆ là:
A. x − 3 = 0
B. x + y − 1 = 0
C. 3 x + 2 y − 5 = 0
D. y − 3 = 0
Cho đường thẳng (d) có phương trình: x- 2y+ 5 0. Có mấy phương trình đường thẳng qua M(2; 1) và tạo với d một góc 450. A. 1 B. 2 C. 3 D. Không có.
Đọc tiếp
Cho đường thẳng (d) có phương trình: x- 2y+ 5= 0. Có mấy phương trình đường thẳng qua M(2; 1) và tạo với d một góc 450.
A. 1
B. 2
C. 3
D. Không có.
Đáp án B
Gọi ∆ là đường thẳng cần tìm và n → ( A ; B ) là VTPT của ∆ A 2 + B 2 ≠ 0
Để ∆ tạo với đường thẳng ( d) một góc 450 thì:
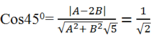
Tương đương: 2( A- 2B) 2= 5( A2+ B2)
Nên A= -3B hoặc B= 3A
+ Với A= - 3B, chọn B= -1 thì A= 3 ta được phương trình ∆ : 3x- y- 5= 0.
+ Với B= 3A, chọn A= 1 thì B= 3 ta được phương trình ∆: x+ 3y- 5 = 0 .
Đúng 0
Bình luận (0)
Cho đường thẳng y=(D1) có phương trình y= x+2, (D2) có phương trình y= -2x+8 ,(D3) có phương trình (m+1)x -m. Tìm m để 3đường thẳng đồng quy.
Gọi A là giao điểm của (D1) và (D2).
Phương trình hoành độ giao điểm của (D1) và D(2)
x + 2 = -2x + 8
--> x = 2
Thay vào (D1) hoặc (D2) tính được y = 4
Để 3 đường thẳng đồng quy, chứng minh điểm A thuộc đường thẳng D(3)
Thay toa độ điểm A vào pt đường thẳng (D3)
4 = (m + 1) . 2 - m
4 = 2m + 2 - m
2 = m
Vậy phương trình đường thẳng (D3) y = 3x - 2 thì ba đường thẳng đồng quy tại A (2; 4)
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy cho đường thẳng d có phương trình x + y - 2 = 0. Hỏi phép vị tự tâm O tỉ số k = -2 biến d thành đường thẳng nào trong các đường thẳng có phương trình sau?
A. 2x + y + 3 = 0
B. 2x + 2y - 4 = 0
C. x + y + 4 = 0
D. x + y - 4 = 0
Trong mặt phẳng Oxy cho đường thẳng d có phương trình x + y - 2 = 0. Hỏi phép vị tự tâm O tỉ số k = -2 biến d thành đường thẳng nào trong các đường thẳng có phương trình sau?
A. 2x + y + 3 = 0
B. 2x + 2y - 4 = 0
C. x + y + 4 = 0
D. x + y - 4 = 0
Trong mặt phẳng Oxy cho đường thẳng d có phương trình 3x − 2y – 6 0a) Viết phương trình của đường thẳng
d
1
là ảnh của d qua phép đối xứng qua trục Oyb) Viết phương trình của đường thẳng
d
2
là ảnh của d qua phép đối xứng qua đường thẳng Δ có phương trình
x
+
y
–
2
0
.
Đọc tiếp
Trong mặt phẳng Oxy cho đường thẳng d có phương trình 3x − 2y – 6 = 0
a) Viết phương trình của đường thẳng d 1 là ảnh của d qua phép đối xứng qua trục Oy
b) Viết phương trình của đường thẳng d 2 là ảnh của d qua phép đối xứng qua đường thẳng Δ có phương trình x + y – 2 = 0 .
a) d 1 : 3x + 2y + 6 = 0
b) Giao của d và Δ là A(2;0). Lấy B(0; −3) thuộc d. Ảnh của B qua phép đối xứng của đường thẳng Δ là B′(5;2). Khi đó d' chính là đường thẳng AB′: 2x − 3y – 4 = 0
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy cho đường thẳng d có phương trình
y
1
3
x
+
2
.Viết phương trình đường thẳng
∆
là ảnh của đường thẳng d qua phép đối xứng trục là đường thẳng yx A.
y
3
x
−
6
B.
y
3
x
+
6
C.
y
-
3
x
+
6...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy cho đường thẳng d có phương trình y = 1 3 x + 2 .Viết phương trình đường thẳng ∆ là ảnh của đường thẳng d qua phép đối xứng trục là đường thẳng y=x
A. y = 3 x − 6
B. y = 3 x + 6
C. y = - 3 x + 6
D. y = - 3 x - 6
Trong mặt phẳng tọa độ Oxy cho đường thẳng d có phương trình
y
1
3
x
+
2
.Viết phương trình đường thẳng
Δ
là ảnh của đường thẳng d qua phép đối xứng trục là đường thẳng yx. A.
y
3
x
−
6
B.
y
3
x
+
6
C.
y
−
3
x
+
6...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy cho đường thẳng d có phương trình y = 1 3 x + 2 .Viết phương trình đường thẳng Δ là ảnh của đường thẳng d qua phép đối xứng trục là đường thẳng y=x.
A. y = 3 x − 6
B. y = 3 x + 6
C. y = − 3 x + 6
D. y = − 3 x − 6
Đáp án A
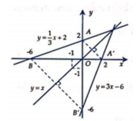
Gọi A 0 ; 2 ; B − 6 ; 0 là hai điểm thuộc đường thằng d. Gọi A' ;B' lần lượt là điểm đối xứng quả A; B qua đường thẳng y=x.
Ta có A ' = 2 ; 0 , B ' 0 ; − 6 (xem hình vẽ)
Phương trình đường thẳng A ' B ' : x 2 + y − 6 = 1 ⇔ y = 3 x − 6
Đúng 0
Bình luận (0)
Bài tập 1. Cho tam giác ABC có A(2;0),B(0;4) , C(1;3) , đường
thẳng Delta / 3 * x - y - 2 0 .
a. Viết phương trình đường cao AH .
b. Viết phương trình đường trung trực của đoạn thẳng BC.
c. Viết phương trình đường thẳng AB.
d. Viết phương trình đường thẳng qua C và có hệ số góc k - 3 . e. Viết phương trình đường trung tuyến kẻ từ C của tam giác ABC.
f. Viết phương trình đường thẳng qua C và song song với đường thẳng AB.
g. Viết phương trình đường thẳng qua B và vuông góc với Delta
h. V...
Đọc tiếp
Bài tập 1. Cho tam giác ABC có A(2;0),B(0;4) , C(1;3) , đường thẳng Delta / 3 * x - y - 2 = 0 . a. Viết phương trình đường cao AH . b. Viết phương trình đường trung trực của đoạn thẳng BC. c. Viết phương trình đường thẳng AB. d. Viết phương trình đường thẳng qua C và có hệ số góc k = - 3 . e. Viết phương trình đường trung tuyến kẻ từ C của tam giác ABC. f. Viết phương trình đường thẳng qua C và song song với đường thẳng AB. g. Viết phương trình đường thẳng qua B và vuông góc với Delta h. Viết phương trình đường thẳng qua C, cắt các tia Ox,Oy^ prime lần lượt tại M, N sao cho OM = 2ON . i. Tìm tọa độ hình chiếu vuông góc của A trên Delta.
Trong mặt phẳng Oxy cho đường thẳng d có phương trình x-2y+2=0 và đường thằng l có phương trình : x - y + 1 = 0. Phép đối xứng trục l biến d thành d’ có phương trình
A. 2x - y - 1 = 0
B. 2x - y + 1 = 0
C. 2x + y + 1 = 0
D. 2x + y - 1 = 0
Gọi giao điểm của d và l là điểm I. Tọa độ điểm I là nghiệm hệ:
x − 2 y + 2 = 0 x − y + 1 = 0 ⇔ x = 0 y = 1 ⇒ I ( 0 ; 1 )
Lấy A(4; 3) thuộc d. Phương trình đường thẳng a qua A và vuông góc với đường thẳng l có vecto chỉ phương là: u a → = n l → = ( 1 ; − 1 ) nên có vecto pháp tuyến là: n a → = ( 1 ; 1 )
Phương trình đường thẳng a: 1( x – 4) + 1.(y – 3) =0 hay x + y – 7 = 0
Gọi H là giao điểm của a và l.Tọa độ H là nghiệm hệ:
x − y + 1 = 0 x + y − 7 = 0 ⇔ x = 3 y = 4 ⇒ H ( 3 ; 4 )
Gọi A’ là điểm đối xứng với A qua H. Khi đó, H là trung điểm của AA’.
Suy ra: x A ' = 2 x H − x A y A ' = 2 y H − y A ⇔ x A ' = 2 y A ' = 5 ⇒ A ' ( 2 ; 5 )
Phương trình đường thẳng IA’: đi qua I(0; 1) và có vecto chỉ phương I A ' → ( 2 ; 4 ) ⇒ n → ( 2 ; − 1 ) . Phương trình IA’:
2( x- 0) - 1(y – 1) = 0 hay 2x – y + 1 = 0 chính là phương trình đường thẳng d’ đối xứng với d qua l.
Đáp án B
Đúng 0
Bình luận (0)