Có bao nhiêu giá trị nguyên dương thỏa mãn (x - 3).(x + 2) = 0
Có bao nhiêu giá trị x nguyên dương thỏa mãn (x - 3).(x + 2) = 0 là:
A. 3
B. 2
C. 0
D. 1
Có bao nhiêu giá trị x nguyên dương thỏa mãn (x-3).(x+2) = 0 là
A. 3
B. 2
C. 0
D. 1
Có bao nhiêu giá trị nguyên dương của x thỏa mãn − 5 3 3 < x < − 24 35 . − 5 6
A. 1
B.0
C.2
D.3
Đáp án cần chọn là: B
Vì x nguyên dương nên x > 0
mà − 5 3 3 = − 125 27 < 0 nên − 5 3 3 < 0 < x < − 24 35 . − 5 6
Khi đó:
0 < x < − 24 35 . − 5 6 0 < x < 4 7
Vì 4 7 < 1 nên 0 < x < 1 nên không có số nguyên dương nào thỏa mãn
Có bao nhiêu giá trị nguyên dương của x thỏa mãn − 4 5 3 < x < − 7 25 . 39 − 14 . 100 78
A.1
B.0
C.2
D.3
Đáp án cần chọn là: B
Vì x nguyên dương nên x > 0 mà − 4 5 3 = − 64 125 < 0 nên − 4 5 3 < 0 < x < − 7 25 . 39 − 14 . 100 78
Khi đó:
0 < x < − 7 25 . 39 − 14 . 100 78 0 < x < 1
Vì 0 < x < 1 nên không có số nguyên dương nào thỏa mãn.
Có bao nhiêu giá trị nguyên dương của x thỏa mãn - 5 3 3 < x < - 24 35 . - 5 6
A. 1
B. 0
C. 2
D. 3
Đáp án là B
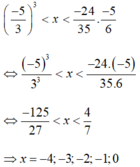
Do yêu cầu đề bài x nguyên dương nên không có giá trị nào thỏa mãn
Có bao nhiêu giá trị nguyên dương của x thỏa mãn bất phương trình log x − 20 + log 40 − x < 2 :
A. 10
B. 20
C. 19
D. 18
Có bao nhiêu giá trị nguyên dương của x thỏa mãn bất phương trình log x - 20 + log 40 - x < 2
A. 19
B. 18
C. 10
D. 20
Đáp án B
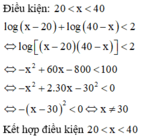
và x nguyên dương, vậy có 18 giá trị của x thỏa mãn đề bài.
Có bao nhiêu giá trị nguyên dương của y để tồn tại số thực x >1 thỏa mãn phương trình: (x2y - 8x + y - 3).log9y = log3\(\dfrac{\sqrt{8x-y+4}}{x}\)
\(\left(x^2y-8x+y-4\right)log_3y=2log_3\dfrac{\sqrt{8x-y+4}}{x}-log_3y=log_3\dfrac{8x-y+4}{x^2y}\)
\(\Rightarrow log_3\left(x^2y\right)+x^2y.log_3y=log_3\left(8x-y+4\right)+\left(8x-y+4\right)log_3y\)
Xét hàm \(f\left(t\right)=log_3t+t.log_3y\Rightarrow f'\left(t\right)=\dfrac{1}{1.ln3}+log_3y>0\)
\(\Rightarrow x^2y=8x-y+4\)
\(\Rightarrow y=\dfrac{8x+4}{x^2+1}\)
Tìm y để pt trên có nghiệm lớn hơn 1, lập BBT \(\Rightarrow y< 6\)
