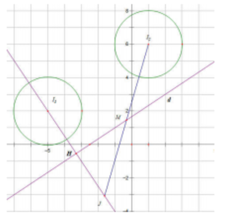
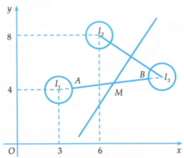
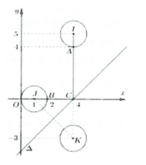
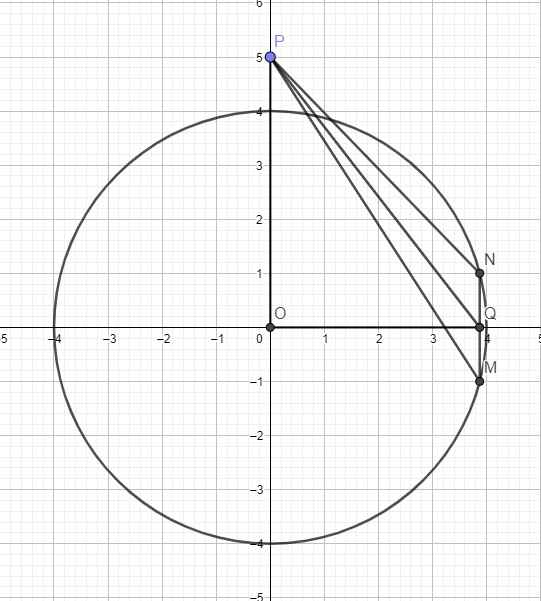
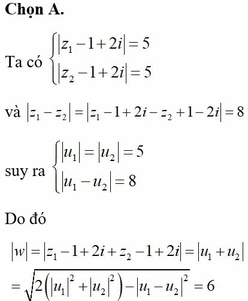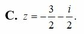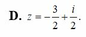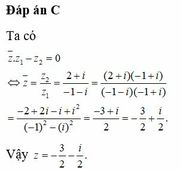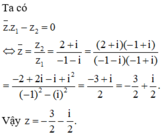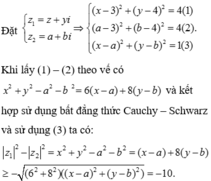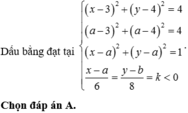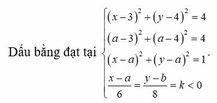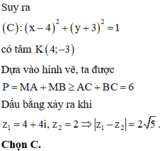Cho số phức z1, z2 thỏa mãn z 1 = z 2 = 2 5 . Gọi M, N lần lượt là điểm biểu diễn hai số phức z1, z2 trên mặt phẳng tọa độ. Biết M N = 2 2 . Gọi H là đỉnh thứ tư của hình bình hành OMHN và K là trung điểm của OM. Tính l=KH
A. l = 3 2
B. l = 6 2
C. l = 41
D. l = 5