Cho ba số phức z 1 , z 2 , z 3 thỏa mãn điều kiện z 1 = z 2 = z 3 = 1 và z 1 + z 2 + z 3 = 0. Tính A = z 1 2 + z 2 2 + z 3 2 .
A. 1
B. 0
C. -1
D. 1 + i
Những câu hỏi liên quan
Cho số phức z thỏa mãn điều kiện
z
-
3
+
2
i
z
-
i
Giả sử w là số phức có môđun nhỏ nhất trong các số phức z thỏa mãn điều kiện trên. Tính môđun của w
Đọc tiếp
Cho số phức z thỏa mãn điều kiện z - 3 + 2 i = z - i Giả sử w là số phức có môđun nhỏ nhất trong các số phức z thỏa mãn điều kiện trên. Tính môđun của w
Cho số phức z thỏa mãn điều kiện
(
3
+
2
i
)
z
+
(
2
-
i
)
2
4
+
i
. Tìm phần ảo của số phức
w
(
1
+
+
z
)
z
¯
. A. -2 B. 0. C. -...
Đọc tiếp
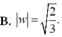
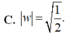
Cho số phức z thỏa mãn điều kiện ( 3 + 2 i ) z + ( 2 - i ) 2 = 4 + i . Tìm phần ảo của số phức w = ( 1 + + z ) z ¯ .
A. -2
B. 0.
C. -1
D. 1
Cho số phức z thỏa mãn điều kiện
(
3
+
2
i
)
z
+
(
2
-
i
)
2
4
+
i
. Tìm phần ảo của số phức
w
(
1
+
z
)
z
¯
.
Đọc tiếp
Cho số phức z thỏa mãn điều kiện ( 3 + 2 i ) z + ( 2 - i ) 2 = 4 + i . Tìm phần ảo của số phức w = ( 1 + z ) z ¯ .
Cho số phức z thỏa mãn điều kiện z + 2 + i z ¯ = 3 + 5 i . Phần thực của số phức z là:
A. -3
B. -2
C. 2
D. 3
Cho số phức z thỏa mãn điều kiện:
z
−
1
z
+
3
−
2
i
. Tập hợp các điểm biểu diễn số phức z là A. Đường thẳng B. Đường tròn C. Một điểm xác định D. Elip
Đọc tiếp
Cho số phức z thỏa mãn điều kiện: z − 1 = z + 3 − 2 i . Tập hợp các điểm biểu diễn số phức z là
A. Đường thẳng
B. Đường tròn
C. Một điểm xác định
D. Elip
Đáp án A
Em hãy thực hiện câu này theo cả 2 cách nhé!
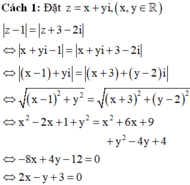
Vậy tập hợp các điểm biểu diễn số phức z là một đường thẳng có phương trình: 2x - y + 3 = 0
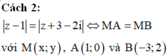
Em thấy, điểm M cách đều hai điểm A, B nên M thuộc đường trung trực của đoạn thẳng AB.
Em có thể tìm phương trình đường trung trực ∆ của đoạn thẳng AB như sau:
AB → = − 4 ; 2 , trung điểm của AB là I − 1 ; 1 , ∆ qua điểm I nhận AB → = − 4 ; 2 làm vectơ pháp tuyến.
Đúng 0
Bình luận (0)
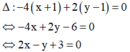
Cho số phức z thỏa mãn điều kiện: |z-1| = |z+3-2i|. Tập hợp các điểm biểu diễn số phức z là
A. Đường thẳng.
B. Đường tròn.
C. Một điểm xác định.
D. Elip.
Đáp án A
Em hãy thực hiện Câu nay theo cả 2 cách nhé!
Cách 1: Đặt 
Cách 2: 
với M(x;y), A(1;0) và B(-3;2)
Em thấy, điểm M cách đều hai điểm A, B nên M thuộc đường trung trực của đoạn thẳng AB.
Em có thể tìm phương trình đường trung trực ∆ của đoạn thẳng AB như sau:
trung điểm của AB là I(-1;1),
∆
qua điểm I nhận 
làm vectơ pháp tuyến.
Đúng 0
Bình luận (0)
Cho số phức z thỏa mãn điều kiện (z+2)(1+2i) 5
z
¯
. Tìm phần ảo của số phức w
(
z
+
2
i
)
2019
A
.
2
1009
B
.
0
C
.
-
2...
Đọc tiếp
Cho số phức z thỏa mãn điều kiện (z+2)(1+2i) = 5 z ¯ . Tìm phần ảo của số phức w = ( z + 2 i ) 2019
A . 2 1009
B . 0
C . - 2 1009
D . 2019
Đáp án A
Đặt z = x + yi với x,y ∈ ℝ , ta có:
= 5x - 5yi
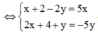
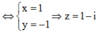
Do đó 
Vậy w có phần ảo bằng 2 1009
Đúng 0
Bình luận (0)
Cho số phức z thỏa mãn điều kiện |z| 1. Tìm giá trị lớn nhất của A |1+z| +3|1-z|
A
.
4
8
B
.
2
15
C
.
10
D
.
2
10
Đọc tiếp
Cho số phức z thỏa mãn điều kiện |z| = 1. Tìm giá trị lớn nhất của A = |1+z| +3|1-z|
A . 4 8
B . 2 15
C . 10
D . 2 10
Trong các số phức z thỏa mãn điều kiện |z – 1 – 2i| 2, tìm số phức z có môđun nhỏ nhất.
Đọc tiếp
Trong các số phức z thỏa mãn điều kiện |z – 1 – 2i| = 2, tìm số phức z có môđun nhỏ nhất.
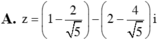
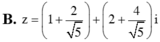
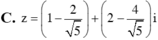
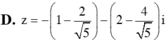
Chọn C.
Gọi z = x + yi và M (x; y) là điểm biểu diễn số phức.
Ta có : |z – 1 – 2i| = 2 hay ( x - 1) 2 + (y - 2)2 = 4
Đường tròn (C): ( x - 1)2 + (y - 2)2 = 4 có tâm I(1; 2). Đường thẳng OI có phương trình y = 2x
Số phức z thỏa mãn điều kiện và có môdun nhỏ nhất khi và chỉ khi điểm biểu diễn số phức đó thuộc đường tròn (C) và gần gốc tọa độ O nhất, điểm đó chỉ là một trong hai giao điểm của đường thẳng OI với (C), khi đó tọa độ của nó thỏa mãn hệ
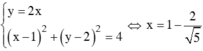hoặc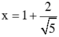 
Chọn 
nên số phức 
Đúng 0
Bình luận (0)
Cho số phức z thỏa mãn điều kiện
z
-
1
2
. Tìm giá trị lớn nhất của
T
z
+
i
+
z
-
2
-
i
A.
m
a
x
T
8
2
B....
Đọc tiếp
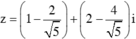
Cho số phức z thỏa mãn điều kiện z - 1 = 2 . Tìm giá trị lớn nhất của T = z + i + z - 2 - i
A. m a x T = 8 2
B. m a x T = 4
C. m a x T = 4 2
D. m a x T = 8 2
