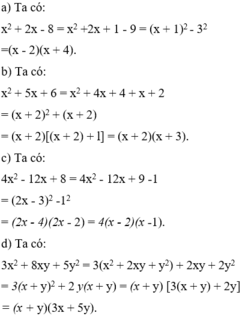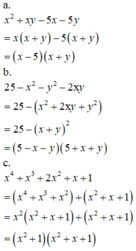Phân tích đa thức sau thành nhân tử: x2 + 5x + 4

Những câu hỏi liên quan
Phân tích đa thức thành nhân tử A = x 2 – 5 x + 4
A. (x - 4).(x - 1)
B. (x – 4).(x + 1)
C. (x + 4).(x + 1)
D. Đáp án khác
Phân tích các đa thức sau thành nhân tử: a)
x
2
+2x-8; b)
x
2
+5x + 6;c) 4
x
2
-12x + 8; d) 3
x
2
+8xy + 5
y
2
.
Đọc tiếp
Phân tích các đa thức sau thành nhân tử:
a) x 2 +2x-8; b) x 2 +5x + 6;
c) 4 x 2 -12x + 8; d) 3 x 2 +8xy + 5 y 2 .
Phân tích các đa thức sau thành nhân tử:
b ) x 3 – x 2 – 5 x + 125
b) x3 – x2 – 5x + 125
= (x3 + 125) - (x2 + 5x)
= (x + 5)(x2 - 5x + 25) - x(x + 5)
= (x + 5)(x2 - 5x + 25 - x)
= (x + 5)(x2 - 6x + 25)
Đúng 0
Bình luận (0)
Phân tích các đa thức sau thành nhân tử:
a) x2 – 3x + 2
b) x2 + x – 6
c) x2 + 5x + 6
Cách 1: Tách một hạng tử thành tổng hai hạng tử để xuất hiện nhân tử chung.
a) x2 – 3x + 2
= x2 – x – 2x + 2 (Tách –3x = – x – 2x)
= (x2 – x) – (2x – 2)
= x(x – 1) – 2(x – 1) (Có x – 1 là nhân tử chung)
= (x – 1)(x – 2)
Hoặc: x2 – 3x + 2
= x2 – 3x – 4 + 6 (Tách 2 = – 4 + 6)
= x2 – 4 – 3x + 6
= (x2 – 22) – 3(x – 2)
= (x – 2)(x + 2) – 3.(x – 2) (Xuất hiện nhân tử chung x – 2)
= (x – 2)(x + 2 – 3) = (x – 2)(x – 1)
b) x2 + x – 6
= x2 + 3x – 2x – 6 (Tách x = 3x – 2x)
= x(x + 3) – 2(x + 3) (có x + 3 là nhân tử chung)
= (x + 3)(x – 2)
c) x2 + 5x + 6 (Tách 5x = 2x + 3x)
= x2 + 2x + 3x + 6
= x(x + 2) + 3(x + 2) (Có x + 2 là nhân tử chung)
= (x + 2)(x + 3)
Cách 2: Đưa về hằng đẳng thức (1) hoặc (2)
a) x2 – 3x + 2
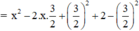
(Vì có x2 và 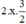 nên ta thêm bớt
nên ta thêm bớt 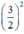 để xuất hiện HĐT)
để xuất hiện HĐT)
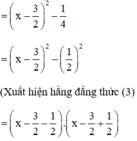
= (x – 2)(x – 1)
b) x2 + x - 6

= (x – 2)(x + 3).
c) x2 + 5x + 6

= (x + 2)(x + 3).
Đúng 0
Bình luận (0)
phân tích các đa thức sau thành nhân tử
a.x2-2x+1
b. x2 5x +xy-5y
a/
\(x^2-2x+1=\left(x-1\right)^2\)
b/
\(x^2-5x+xy-5y=x\left(x+y\right)-5\left(x+y\right)=\)
\(=\left(x+y\right)\left(x-5\right)\)
Đúng 0
Bình luận (0)
Phân tích các đa thức sau thành nhân tử :
i/ x2+5x−6x2+5x−6
m/ 6x2−7x+26x2−7x+2
n/ 4x4+81
a: =(x+6)(x-1)
n: \(=4x^4+36x^2+81-36x^2\)
\(=\left(2x^2+9-6x\right)\left(2x^2+9+6x\right)\)
Đúng 1
Bình luận (0)
phân tích đa thức sau thành nhân tử
2x3-5xx2x2+6x-15
À mình nhầm 5xx2x2 chuyển thành 5x2
Đúng 0
Bình luận (0)
Ghi lại đề bài được ko bạn ? Mình chưa hiểu cho lắm !!!
Đúng 0
Bình luận (0)
2x^3-5x^2+6x-15
=(2x^3+6x)-(5x^2+15)
=2x(x^2+3)-5(x^2+3)
=(x^2+3)(2x-5)
Đúng 0
Bình luận (0)
Phân tích các đa thức sau thành nhân tửa)
x
2
+
x
y
−
5
x
−
5
y
b)
25
−
x
2
−
y
2
−
2
x
y
c)
x
4
+
x
3
+
2
x
2
+...
Đọc tiếp
Phân tích các đa thức sau thành nhân tử
a) x 2 + x y − 5 x − 5 y
b) 25 − x 2 − y 2 − 2 x y
c) x 4 + x 3 + 2 x 2 + x + 1
Chứng tỏ rằng nếu phương trình ax2 + bx + c = 0 có nghiệm là x1 và x2 thì tam thức ax2 + bx + c phân tích được thành nhân tử như sau:
ax2 + bx + c = a( x - x1)(x - x2)
Áp dụng : phân tích đa thức thành nhân tử.
2x2 - 5x + 3
* Chứng minh:
Phương trình ax2 + bx + c = 0 có hai nghiệm x1; x2
⇒ Theo định lý Vi-et: 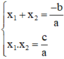
Khi đó : a.(x – x1).(x – x2)
= a.(x2 – x1.x – x2.x + x1.x2)
= a.x2 – a.x.(x1 + x2) + a.x1.x2
= 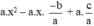
= a.x2 + bx + c (đpcm).
* Áp dụng:
a) 2x2 – 5x + 3 = 0
Có a = 2; b = -5; c = 3
⇒ a + b + c = 2 – 5 + 3 = 0
⇒ Phương trình có hai nghiệm 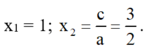
Vậy: 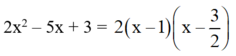
Đúng 0
Bình luận (0)