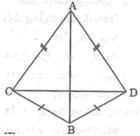
Cho hình bên. Chứng minh rằng AB vuông góc với CD.
Những câu hỏi liên quan
Cho hình thang cân ABCD (AB // CD), AB=BC và BC vuông góc với BD.
a) Chứng minh AC vuông góc với AD
b) Tính số đo các góc còn lại
c) Gọi o là giao điểm của hai đường chéo. Chứng minh rằng O cách đều hai cạnh bên và đáy lớn
1. Cho hình thang ABCD có góc A góc D 90 độ , đáy nhỏ AB a , cạnh bên BC 2 a . Gọi M , N lần lượt là trung điểm AD , ABa / Tính số đo các góc ABC , BANb/ Chứng minh tam giác NAD đềuc/ Tính MN theo a 2. a/ Tính các góc A , góc B của hình thang ABCD ( AB // CD ) biết góc C 70 độ , góc D 40 độb/ Cho hình thang ABCD có AB // CD và góc A góc D . Chứng minh rằng ABCD là hình thang vuông cà AC^2 + BD^2 AB^2 + CD^2 + 2AD^23. Cho tứ giác ABCD :a/ Chứng minh rằng AB + CD AC + BDb/ Cho biết AB + B...
Đọc tiếp
1. Cho hình thang ABCD có góc A = góc D = 90 độ , đáy nhỏ AB = a , cạnh bên BC = 2 a . Gọi M , N lần lượt là trung điểm AD , AB
a / Tính số đo các góc ABC , BAN
b/ Chứng minh tam giác NAD đều
c/ Tính MN theo a
2. a/ Tính các góc A , góc B của hình thang ABCD ( AB // CD ) biết góc C = 70 độ , góc D = 40 độ
b/ Cho hình thang ABCD có AB // CD và góc A = góc D . Chứng minh rằng ABCD là hình thang vuông cà AC^2 + BD^2 = AB^2 + CD^2 + 2AD^2
3. Cho tứ giác ABCD :
a/ Chứng minh rằng AB + CD < AC + BD
b/ Cho biết AB + BD < hoặc = AC + CD
Chứng minh rằng AB < AC
4. Cho hình thang ABCD có AC vuông góc BD . CHứng minh rằng :
a/ AB^2 + CD^2 = AD^2 + BC^2
b/ ( AB + CD )^2 = AC^2 + BD^2
bạn hỏi thế này thì chả ai muốn làm -_- dài quá
Đúng 1
Bình luận (0)
Bạn gửi từng câu nhò thì các bạn khác dễ làm hơn!
Đúng 1
Bình luận (0)
dài quà làm sao mà có thòi gian mà trả lời .bạn hỏi ít thoi chứ
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Cho hình thang ABCD (AB//CD), góc D 90 độ, góc C bằng 30 độa) Chứng minh rằng diện tích hình thanh ABCD 1/4*BC*(AB+CD)b) Gọi M là giao điểm của BC và AD. Kẻ DK vuông góc với CM (K thuộc CM), KL vuông góc với DM (L thuộc DM). Chứng minh rằng 4*DL*DMCD2 c) Biết BC 8cm, diện tích hình thang ABCD 48 cm2. Tính DM, MC (không làm tròn kết quả)Mng giúp mik với, mai mik ktra rồi
Đọc tiếp
Cho hình thang ABCD (AB//CD), góc D = 90 độ, góc C bằng 30 độ
a) Chứng minh rằng diện tích hình thanh ABCD = 1/4*BC*(AB+CD)
b) Gọi M là giao điểm của BC và AD. Kẻ DK vuông góc với CM (K thuộc CM), KL vuông góc với DM (L thuộc DM). Chứng minh rằng 4*DL*DM=CD2
c) Biết BC = 8cm, diện tích hình thang ABCD = 48 cm2. Tính DM, MC (không làm tròn kết quả)
Mng giúp mik với, mai mik ktra rồi
1) Cho hình thang cân ABCD (AB // CD). a) Chứng minh:. b) Gọi E là giao điểm của AC và BD. Chứng minh: . 2) Cho hình thang cân ABCD có đáy nhỏ CD = a , . Đường chéo AC vuông góc với cạnh bên BC. a) Tính các góc của hình thang. b) Chứng minh AC là phân giác của góc . c) Tính diện tích của hình thang.
Cho hình thang cân ABCD(AB//CD), AB=BC và BC vuông góc với BD
a) Chứng minh AC vuông góc với AD
b) Tính số đo các góc hình thang
c) Gọi O là giao điểm của 2 đường chéo. Chứng minh rằng O cách đều 2 cnhj bên và đáy lớn
d) Gọi M là giao điểm cảu AD và Bc. H là hình chiếu của O trên DC. Chứng minh M,H,O thẳng hàng
Cho hình bình hành ABCD. Kẻ AM vuông góc với BC, AN vuông góc với CD.
a, Chứng minh rằng AM : AN = AB : BC.
b, Gọi I, J lần lượt là trung điểm của AB, AD. Chứng minh rằng diện tích hình ABCD = 2 lần diện tích hình AICJ.
Cho hình thang cân ABCD (AB // CD , AB>CD) có CD=a , A + B = 1/2(C+D) Đường chéo AC vuông góc với cạnh bên BC.
A) Tính các góc của hình thang
B) Chứng minh AC là phân giác góc DAB
a) Ta có ABCD là hình thang cân
=> \(\widehat{D}=\widehat{C},\widehat{A}=\widehat{B}\)(1)
Mà: \(\widehat{A}+\widehat{B}=\frac{1}{2}\left(\widehat{C}+\widehat{D}\right)\)(2)
Từ (1), (2)
=> \(2.\widehat{A}=\frac{1}{2}.2.\widehat{D}\Leftrightarrow\widehat{D}=2.\widehat{A}\)(3)
Mặt khác: \(\widehat{A}+\widehat{D}=180^o\)(4)
Từ (3), (4)
=> \(\widehat{A}=60^o\Rightarrow\widehat{D}=120^o\)
=> \(\widehat{B}=60^o;\widehat{C}=60^o\)
b) Ta có: \(\widehat{C}=\widehat{C_1}+\widehat{C_2}\Rightarrow\widehat{C_1}=\widehat{C}-\widehat{C_2}=120^o-90^o=30^o\)
=> \(\widehat{A_1}=\widehat{C_1}=30^o\left(soletrong\right)\)
Mà \(\widehat{A}=\widehat{A_1}+\widehat{A_2}\Rightarrow\widehat{A_2}=30^o\)
Từ 2 điều trên suy ra góc A1 = góc A2
=> AC là phân giác góc DAB
Đúng 1
Bình luận (0)
Cho hình thang cân ABCD (AB//CD, AB>CD) có CD=a, góc A cộng góc B=1/2 (góc C cộng góc D). Đường chéo AC vuông góc với cạnh bên BC.
a) Tính các góc của hình thang
b) Chứng minh AC là phân giác của góc DAB.
Bài 1. Cho hình thang ABCD cân (AB // CD, AB < CD), kẻ AE vuông góc CD tại E, BF vuông góc CD tại F. Chứng minh rằng: a) DE = CF, DF = CE b) Chứng minh tứ giác ABFE là hình chữ nhật, từ đó suy ra AF = BE.
a: Xét ΔAED vuông tại E và ΔBFC vuông tại F có
AD=BC
\(\widehat{D}=\widehat{C}\)
Do đó: ΔAED=ΔBFC
Suy ra: DE=FC
Đúng 0
Bình luận (1)