Tìm các số phức z thỏa mãn: z 3 + z ¯ = 0
A. z = 0
B. z = ± 1
C. z = ± i
D. Tất cả đúng.
Những câu hỏi liên quan
Tìm các số phức z thỏa mãn
z
2
+
3
(
1
-
2
i
)
z
-
4
+
6
i
0
. A.
z
1
-
1
;
z
2
-
4
+
6
i
B.
z
1
1...
Đọc tiếp
Tìm các số phức z thỏa mãn z 2 + 3 ( 1 - 2 i ) z - 4 + 6 i = 0 .
A. z 1 = - 1 ; z 2 = - 4 + 6 i
B. z 1 = 1 ; z 2 = - 4 + 6 i
C. z 1 = 1 ; z 2 = - 4 - 6 i
D. z 1 = - 1 ; z 2 = - 4 - 6 i
Tìm các số phức z thỏa mãn
z
2
+
3
(
1
-
2
i
)
z
-
4
+
6
i
0
Đọc tiếp
Tìm các số phức z thỏa mãn z 2 + 3 ( 1 - 2 i ) z - 4 + 6 i = 0
Số phức z thỏa mãn z^6-z^5+z^4-z^3+z^2-z+1=0. Tìm phần thực của w=z(z^2-z+1).
Cho số phức z thỏa mãn \(z^6-z^5+z^4-z^3+z^2-z+1=0\)Tìm phần thực của \(w=z\left(z^2-z+1\right)\)
Tìm số phức z có phần ảo dương thỏa mãn
z
¯
−
3
−
2
i
z
−
2
i
0
. Khi đó |z| bằng A.
z
5
−
2
3
B.
z
5...
Đọc tiếp
Tìm số phức z có phần ảo dương thỏa mãn z ¯ − 3 − 2 i z − 2 i = 0 . Khi đó |z| bằng
A. z = 5 − 2 3
B. z = 5 − 3
C. z = 5 + 2 3
D. z = 4 − 2 3
Cho số phức z a+bi; a,bϵR; a0 thỏa mãn
z
-
1
+
z
-
2
a
b
Tính
z
1
+
z
-
A. ...
Đọc tiếp
Cho số phức z = a+bi; a,bϵR; a>0 thỏa mãn z - 1 + z - 2 = a = b Tính z 1 + z -
A. 3 2
B. 10
C. 5
D. 2
Tìm số phức z thỏa mãn: (1+iz)(3-i)-(2+5i)(z-i) = 0
A. z = 1 - i
B. z = 1 + i
C. z = - i
D. z = i
Cho số phức z thỏa mãn điều kiện (1+i) z ¯ - 1 - 3i = 0. Tìm phần ảo của số phức w = 1 - zi + z ¯
A. -i
B. -1
C. 2
D. -2i
Đáp án C
giả sử 
The giả thiết, ta có
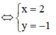
Suy ra 
Ta có 
Vậy chọn phần ảo là – 1
Đúng 0
Bình luận (0)
Cho số phức z = a + bi(a,b ∈ ℝ ) thỏa mãn z + 2 + i - |z|(1+i) = 0 và |z| > 1. Tính P = a + b
A. P = -1
B. P = -5
C. P = 3
D. P = 7
Đáp án D.
Đặt z = a + bi => a + bi 
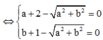
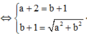
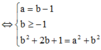
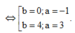
Do |z| > 1 => a = 3, b = 4
Đúng 0
Bình luận (0)