hông hỉu      

^o^;^-^;-_-;0o0

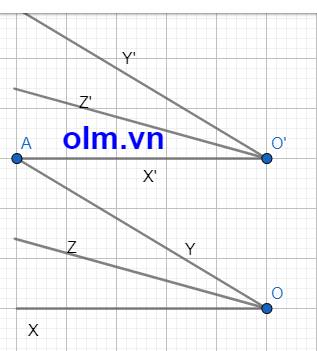
a,Kéo dài OY cắt O'X' tại A ta có: 

  \(\widehat{XOY}\) =  \(\widehat{XOA}\)  = \(\widehat{OAO'}\) (so le trong) (1)

   \(\widehat{Y'O'X'}\) = \(\widehat{Y'O'A}\) = \(\widehat{OAO'}\) (so le trong) (2)

Kết hợp (1) Và (2) ta có:

    \(\widehat{XOY=}\) \(\widehat{X'O'Y'}\) (đpcm)

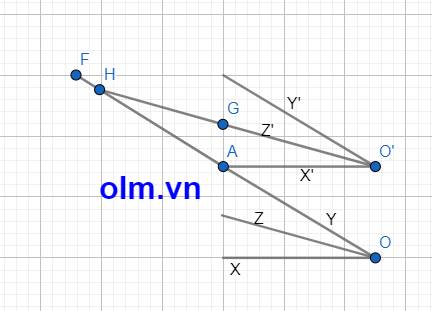
b, Kéo dài OY cắt O'Z' tại H 

             \(\widehat{ZOA}\) = \(\dfrac{1}{2}\) \(\widehat{XOY}\) (vì OZ là phân giác của góc XOY

             \(\widehat{HO'A}\) = \(\dfrac{1}{2}\) \(\widehat{X'O'Y'}\) (vì OY là phân giác của góc X'O'Y')

         Mặt khác ta có \(\widehat{OAO'}\) = \(\widehat{HO'A}\) + \(\widehat{AHO'}\) (góc ngoài tam giác bằng tổng hai góc trong không kề với nó)

               \(\widehat{HO'A}\) = \(\dfrac{1}{2}\) \(\widehat{OAO'}\)  ⇒ \(\widehat{AHO'}\) = \(\dfrac{1}{2}\) \(\widehat{OAO'}\) = \(\dfrac{1}{2}\) \(\widehat{XOY}\)

          ⇒ \(\widehat{ZOA}\) = \(\widehat{AHO'}\) (hai góc này ở vị trí so le trong)

         ⇒ OZ // O'Z' (đpcm)

cửa hàng bán được một tạ rưỡi gẹo tẻ và gạo nếp ; trong đó 25% là gạo nếp. hỏi của hàng bán mỗi loại bao nhiêu ki-lô-gam gạo

fs

a)xOy=xOA+AOy(vì là 2 góc kề bù)

90=60+AOy

AOy=90-60

AOy=30

=> OA là tia phân giác của yOB 

xOy=yOB+BOA(vì là 2 góc kề bù)

90=60+BOA

BOA=90-60

BOA=30

=>OB là tia phân giác của xOA(vì tia phân giác bằng 60:2=30)

b)

a) Ta có: \(\widehat{xOy}=140^0\)

              \(\widehat{xOA}=\widehat{yOB}=90^0\) ( do \(OA\perp Ox,OB\perp Oy\) )

\(\Rightarrow\widehat{AOB}=360-\left(\widehat{xOy}+\widehat{xOA}+\widehat{yOB}\right)\)

\(\Leftrightarrow\widehat{AOB}=360^0-\left(140^0+90^0+90^0\right)\)

\(\Leftrightarrow\widehat{AOB}=40^0\)

\(OM\) là tia phân giác của \(\widehat{xOy}\)

\(\Rightarrow\widehat{xOM}=\widehat{MOy}=\dfrac{1}{2}\widehat{xOy}=\dfrac{1}{2}.140^0=70^0\)

\(OM'\) là tia đối của \(OM\Rightarrow\widehat{MOM'}=180^0\)

Mà \(OA\) nằm ngoài \(\widehat{xOy}\) và \(OA\perp Ox\) nên \(\widehat{MOM'}=\widehat{MOx}+\widehat{xOA}+\widehat{AOM'}\)

Do đó \(\widehat{AOM'}=\widehat{MOM'}-\left(\widehat{MOx}+\widehat{xOA}\right)\) \(\Rightarrow\widehat{AOM'}=180^0-\left(70^0+90^0\right)=20^0\) \(\left(1\right)\)

Mặt khác \(Oy\) nằm giữa \(OB\) và \(OM\) nên \(\widehat{MOB}=\widehat{MOy}+\widehat{yOB}=70^0+90^0=160^0\)

\(\Rightarrow\widehat{MOB}< \widehat{MOM'}\)

Do đó \(OB\) và \(Oy\) nằm cùng nửa mặt phẳng bờ \(MM'\)

\(Ox\) nằm giữa \(OA\) và \(OM\) nên\(\widehat{MOA}=\widehat{MOx}+\widehat{xOA}=70^0+90^0=160^0\) 

\(\Rightarrow\widehat{MOA}< \widehat{MOM'}\) 

Do đó tia \(OA\) và \(Ox\) nằm cùng nửa mặt phẳng bờ \(MM'\)

Nên \(OM'\) nằm giữa \(OA\) và \(OB\)

\(\Rightarrow\widehat{AOB}=\widehat{AOM'}+\widehat{M'OB}\Rightarrow\widehat{M'OB}=\widehat{AOB}-\widehat{AOM'}=40^0-20^0=20^0\left(2\right)\) 

Từ \(\left(1\right)\) và \(\left(2\right)\) ta có: \(\widehat{M'OB}=\widehat{AOM'}=20^0=\dfrac{1}{2}\widehat{AOB}\)

Suy ra \(OM'\) là tia phân giác của góc \(\widehat{AOB}\)

b) Ta có: \(\widehat{MOx}< \widehat{MOA}< \widehat{MOM'}\) nên \(OA\) nằm giữa \(Ox\) và \(OM'\)

Mà \(OM'\) là tia phân giác của góc \(\widehat{AOB}\) 

Suy ra \(OA\) nằm giữa \(Ox\) và \(OB\)

Vậy \(\widehat{xOB}=\widehat{xOA}+\widehat{AOB}=90^0+40^0=130^0\)

dsa

a) Suy ra OM' là tia phân giác của góc AOB.

b) Vậy góc xOB = góc xOA + góc AOB = 90^o + 40^o = 130^o.

M.n vẽ cả hình hộ mk nha!

4

Giải:

Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)

\(\Rightarrow\widehat{A}+\widehat{B}+30^o=180^o\)

\(\Rightarrow\widehat{A}+\widehat{B}=150^o\)

a) Ta có: \(\widehat{A}+\widehat{B}=150^o\)

\(\Rightarrow x+y=150^o\)

Mà x = 2y

\(\Rightarrow2y+y=150^o\)

\(\Rightarrow3y=150^o\)

\(\Rightarrow y=50^o\)

\(\Rightarrow x=50^o.2=100^o\)

Vậy \(y=50^o,x=100^o\)

b) Ta có: \(\widehat{A}+\widehat{B}=150^o\)

\(\Rightarrow x+y=150^o\)

Mà \(x-y=10^o\)

\(\Rightarrow x=\left(150^o+10^o\right):2=80^o\)

\(\Rightarrow y=150^o-80^o=70^o\)

Vậy \(x=80^o,y=70^o\)

c) Ta có: \(3x=2y\Rightarrow\frac{x}{3}=\frac{y}{2}\) và \(\widehat{A}+\widehat{B}=150^o\) hay \(x+y=150^o\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x}{3}=\frac{y}{2}=\frac{x+y}{3+2}=\frac{150^o}{5}=30^o\)

+) \(\frac{x}{3}=30^o\Rightarrow x=90^o\)

+) \(\frac{y}{2}=30^o\Rightarrow y=60^o\)

Vậy \(x=90^o,y=60^o\)

a)

Xét \(\Delta AOD\) và \(\Delta COB\) có: \(\left\{{}\begin{matrix}OA=OC\left(gt\right)\\\widehat{O}:chung\\OB=OD\left(gt\right)\end{matrix}\right.\)

\(\Rightarrow\Delta AOD=\Delta COB\left(c.g.c\right)\)

\(\Rightarrow AD=BC\left(\text{2 cạnh tương ứng}\right)\left(\text{đpcm}\right)\)

b) 

Nối A với C

Ta có: \(\left\{{}\begin{matrix}OA=OC\\OB=OD\end{matrix}\right.\left(gt\right)\Rightarrow OA-OB=OC-OD\)

Hay \(AB=CD\)

Xét \(\Delta ABC\) và \(\Delta CDA\) có: \(\left\{{}\begin{matrix}AB=CD\left(cmt\right)\\AC:chung\\AD=BC\left(cmt\right)\end{matrix}\right.\)

\(\Rightarrow\Delta ABC=\Delta DCA\left(c.c.c\right)\)

\(\Rightarrow\widehat{ABC}=\widehat{CDA}\left(\text{2 góc tương ứng}\right)\)

Vì \(\Delta AOD=\Delta COB\left(cmt\right)\Rightarrow\widehat{A}=\widehat{C}\left(\text{2 góc tương ứng}\right)\)

Xét \(\Delta ABE\) và \(\Delta CDE\) có: \(\left\{{}\begin{matrix}\widehat{ABC}=\widehat{CDA}\left(cmt\right)\\AB=CD\left(cmt\right)\\\widehat{A}=\widehat{C}\left(cmt\right)\end{matrix}\right.\)

\(\Rightarrow\Delta ABE=\Delta CDE\left(g.c.g\right)\left(\text{đpcm}\right)\)

c) Vì \(\Delta ABE=\Delta CDE\left(cmt\right)\Rightarrow AE=CE\left(\text{2 cạnh tương ứng}\right)\)

Xét \(\Delta AOE\) và \(\Delta COE\) có: \(\left\{{}\begin{matrix}OA=OC\left(gt\right)\\\widehat{A}=\widehat{C}\left(cmt\right)\\AE=CE\left(cmt\right)\end{matrix}\right.\)

\(\Rightarrow\Delta AOE=\Delta COE\left(c.g.c\right)\\ \Rightarrow\widehat{AOE}=\widehat{COE}\left(\text{2 góc tương ứng}\right)\)

`=> OE` là phân giác của \(\widehat{xOy}\) (đpcm)

a) Xét $△OAD$ và $△OCB$, có

$OA=OC$ (giả thiết);

�^O chung;

$OD=OB$ (giả thiết).

Do đó $△OAD=△OCB$ (c.g.c)

$\Rightarrow AD=CB$ (hai cạnh tương ứng).

b) Do $OA=OC$ và $OB=OD$ nên $AB=CD$.

Mà $△OAD=△OCB$ (chứng minh trên)

⇒���^=���^⇒OBC=ODA; ���^=���^OAD=OCB (hai góc tương ứng)

Mặt khác ���^+���^=���^+���^=180∘ABE+OBC=CDE+ODA=180∘

⇒���^=���^⇒ABE=CDE

Xét $△ABE$ và $△CDE$ có

���^=���^OAD=OCB (chứng minh trên);

$AB=CD$ (chứng minh trên);

���^=���^ABE=CDE (chứng minh trên) 

Do đó $△ABE=△CDE$ (g.c.g).

c) Vi $△ABE=△CDE$ (chứng minh trên) nên $AE=CE$ (hai cạnh tương ứng).

Xét $△AEO$ và $△CEO$ có $AE=CE$ (chứng minh trên);

$OE$ cạnh chung;

$OA=OC$ (giả thiết).

Do đó △���=△���$△AEO=△CEO$ (c.c.c)

⇒���^=���^⇒AOE=

COE

$\hat{}$ (hai góc tương ứng)

$\Rightarrow OE$ là tia phân giác của ���^xOy​.

a) Xét $△OAD$ và $△OCB$, có

$OA=OC$ (giả thiết);

�^O chung;

$OD=OB$ (giả thiết).

Do đó $△OAD=△OCB$ (c.g.c)

$\Rightarrow AD=CB$ (hai cạnh tương ứng).

b) Do $OA=OC$ và $OB=OD$ nên $AB=CD$.

Mà $△OAD=△OCB$ (chứng minh trên)

⇒���^=���^⇒OBC=ODA; ���^=���^OAD=OCB (hai góc tương ứng)

Mặt khác ���^+���^=���^+���^=180∘ABE+OBC=CDE+ODA=180∘

⇒���^=���^⇒ABE=CDE

Xét $△ABE$ và $△CDE$ có

���^=���^OAD=OCB (chứng minh trên);

$AB=CD$ (chứng minh trên);

���^=���^ABE=CDE (chứng minh trên) 

Do đó $△ABE=△CDE$ (g.c.g).

c) Vi $△ABE=△CDE$ (chứng minh trên) nên $AE=CE$ (hai cạnh tương ứng).

Xét $△AEO$ và $△CEO$ có $AE=CE$ (chứng minh trên);

$OE$ cạnh chung;

$OA=OC$ (giả thiết).

Do đó $△AEO=△CEO$ (c.c.c)

⇒���^=���^⇒AOE=COE (hai góc tương ứng)

$\Rightarrow OE$ là tia phân giác của ���^xOy​.