Trong không gian Oxyz, cho tam giác ABC, biết A 1 ; - 2 ; 4 , B 0 ; 2 ; 5 , C 5 ; 6 ; 3 . Tọa độ trọng tâm G của tam giác ABC là
A. G 2 ; 2 ; 4
B. G 4 ; 2 ; 2
C. G 3 ; 3 ; 6
D. G 3 ; 3 ; 6
Những câu hỏi liên quan
Trong không gian Oxyz, cho tam giác ABC, biết A(1;-2;4), B(0;2;5), C(5;6;3). Tọa độ trọng tâm G của tam giác ABC là A. G(2;2;4) B. G(4;2;2) C. G(3;3;6) D. G(6;3;3)
Đọc tiếp
Trong không gian Oxyz, cho tam giác ABC, biết A(1;-2;4), B(0;2;5), C(5;6;3). Tọa độ trọng tâm G của tam giác ABC là
A. G(2;2;4)
B. G(4;2;2)
C. G(3;3;6)
D. G(6;3;3)
Trong không gian với hệ trục tọa độ Oxyz, cho tam giác ABC biết
A
(
3
;
1
;
2
)
,
B
(
1
;
−
4
;
2
)
,
C
(
2
;
0
;
−
1
)
.
Tìm tọa độ tâm G của tam giác ABC A. G (2;-1;1). B. G (6;-3;3). C. G (2;1;1). D. G (2;-1;3).
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho tam giác ABC biết A ( 3 ; 1 ; 2 ) , B ( 1 ; − 4 ; 2 ) , C ( 2 ; 0 ; − 1 ) . Tìm tọa độ tâm G của tam giác ABC
A. G (2;-1;1).
B. G (6;-3;3).
C. G (2;1;1).
D. G (2;-1;3).
Trong không gian Oxyz, cho tam giác ABC trong đó A(1;0;-2), B(2;1;-1), C(1;-2;2) Tìm tọa độ trọng tâm G của tam giác ABC.
Đọc tiếp
Trong không gian Oxyz, cho tam giác ABC trong đó A(1;0;-2), B(2;1;-1), C(1;-2;2) Tìm tọa độ trọng tâm G của tam giác ABC.
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A(0;1;1), B(1;-2;0), C(-2;1;-1). Diện tích tam giác ABC là
Đọc tiếp
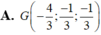
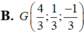
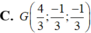
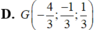
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A(0;1;1), B(1;-2;0), C(-2;1;-1). Diện tích tam giác ABC là
Trong không gian tọa độ Oxyz, cho tam giác ABC biết A (1;0;-1), B (2;3;-1), C (-2;1;1). Phương trình đường thẳng đi qua tâm đường tròn ngoại tiếp của tam giác ABC và vuông góc với mặt phẳng (ABC) là:
Đọc tiếp
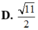
Trong không gian tọa độ Oxyz, cho tam giác ABC biết A (1;0;-1), B (2;3;-1), C (-2;1;1). Phương trình đường thẳng đi qua tâm đường tròn ngoại tiếp của tam giác ABC và vuông góc với mặt phẳng (ABC) là:
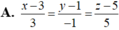
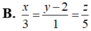
Chọn A
Ta có:
AB² = 10, BC² = 24, AC² = 14 => ∆ABC vuông tại A.
Tâm I của đường tròn ngoại tiếp tam giác là trung điểm của BC => I (0;2;0).
Đường thẳng d cần tìm đi qua I (0;2;0) và nhận vectơ 
làm véc tơ chỉ phương. Phương trình chính tắc của đường thẳng d là 
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz cho tam giác ABC biết
A
2
;
1
,
0
;
B
3
,
0
,
2
;
C
4
,
3
,
-
4
. Viết phư...
Đọc tiếp
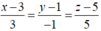
Trong không gian với hệ tọa độ Oxyz cho tam giác ABC biết A 2 ; 1 , 0 ; B 3 , 0 , 2 ; C 4 , 3 , - 4 . Viết phương trình đường phân giác trong góc A.
A. x = 2 y = 1 + t z = 0
B. x = 2 y = 1 z = t
C. x = 2 + t y = 1 z = 0
D. x = 2 + t y = 1 z = t
Giả sử đường phân giác trong của góc A cắt cạnh BC tại D.
Ta có
phương trình BC là:
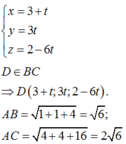
Áp dụng tính chất đường phân giác ta có:
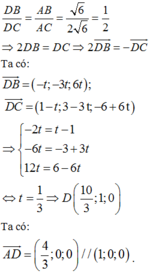
Vậy phương trình đường thẳng
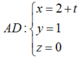
Chọn C.
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho tam giác ABC trong đó A(1; 0; -2), B(2; 1; -1), C(1; -2; 2). Tìm tọa độ trọng tâm G của tam giác ABC A.
G
(
-
4
3
;
-
1
3
;
-
1
3
)
B.
G
(
4
3
;...
Đọc tiếp
Trong không gian Oxyz, cho tam giác ABC trong đó A(1; 0; -2), B(2; 1; -1), C(1; -2; 2). Tìm tọa độ trọng tâm G của tam giác ABC
A. G ( - 4 3 ; - 1 3 ; - 1 3 )
B. G ( 4 3 ; 1 3 ; - 1 3 )
C. G ( 4 3 ; - 1 3 ; - 1 3 )
D. G ( 4 3 ; - 1 3 ; 1 3 )
Trong không gian tọa độ Oxyz, cho tam giác ABC biết A (1; 0; -1), B (2; 3; -1), C (-2; 1; 1). Phương trình đường thẳng đi qua tâm đường tròn ngoại tiếp của tam giác ABC và vuông góc với mặt phẳng (ABC) là:
A
.
x
3
y
-
2
-
1
z
5
B
.
...
Đọc tiếp
Trong không gian tọa độ Oxyz, cho tam giác ABC biết A (1; 0; -1), B (2; 3; -1), C (-2; 1; 1). Phương trình đường thẳng đi qua tâm đường tròn ngoại tiếp của tam giác ABC và vuông góc với mặt phẳng (ABC) là:
A . x 3 = y - 2 - 1 = z 5
B . x 3 = y - 2 1 = z 5
C . x - 1 1 = y - 2 = z + 1 2
D . x - 3 3 = y - 2 - 1 = z - 5 5
Chọn A
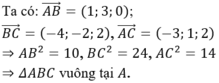
Tâm I của đường tròn ngoại tiếp tam giác là trung điểm của BC => I (0; 2; 0)
Đường thẳng d cần tìm đi qua I (0; 2; 0) và nhận vectơ 
làm véc tơ chỉ phương. Phương trình chính tắc của đường thẳng d là 
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho tam giác ABC với A(1;2;3),B(-10;-5;-1),C(-3;-9;10). Phương trình đường phân giác kẻ từ đỉnh A của tam giác ABC là A.
x
-
1
3
y
-
2
-
2
z
-
3...
Đọc tiếp
Trong không gian Oxyz, cho tam giác ABC với A(1;2;3),B(-10;-5;-1),C(-3;-9;10). Phương trình đường phân giác kẻ từ đỉnh A của tam giác ABC là
A. x - 1 3 = y - 2 - 2 = z - 3 3
B. x - 1 - 3 = y - 2 - 2 = z - 3 7
C. x - 1 1 = y - 2 - 1 = z - 3 - 1
D. x - 1 - 5 = y - 2 - 6 = z - 3 1
