Hàm số nào sau đây không có giá trị nhỏ nhất và giá trị lớn nhất trên đoạn − 2 ; 2 ?
A. y = x 3 + 2.
B. y = x 4 + x 2 .
C. y = − x + 1.
D. y = x − 1 x + 1 .
Hàm số nào không có giá trị nhỏ nhất và giá trị lớn nhất trên đoạn [-3;1]?
A. y = x 3 + 2
B. y = x 4 + x 2
C. y = x − 1 x + 1
D. y = x + 1 x − 2
Hàm số nào không có giá trị nhỏ nhất và giá trị lớn nhất trên đoạn − 3 ; 1 ?
A. y = x 3 + 2
B. y = x 4 + x 2
C. y = x − 1 x + 1
D. y = x + 1 x − 2
Đáp án C
Nhận thấy hàm số y = x − 1 x + 1 không xác định tại x = − 1 ∈ − 3 ; 1
Gọi M, n lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x 2 - 3 x - 2 trên đoạn [ - 1 ; 3 2 ] . Mệnh đề nào sau đây là đúng?
A. M+n = 8 3
B. M+n = 7 2
C. M+n = 13 6
D. M+n = 4 3
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x + m x + 1 trên đoạn [1;2] bằng 8 (m là tham số thực). Khẳng định nào sau đây là đúng?
A. 0 < m < 4
B. 4 < m < 8
C. 8 < m < 10
D. m > 10

Vì hàm số đã cho là hàm bậc nhất trên bậc nhất nên hàm số đơn điệu trên từng khoảng xác định của hàm số.
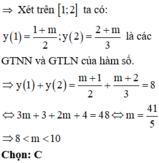
Hàm số nào sau đây có giá trị nhỏ nhất trên đoạn [0;2] bằng –2?
A. y = x 3 - 10
B. y = x + 2 - 2
C. y = x - 2 x + 1
D. y = 2 x - 2
Đáp án C
Phương pháp:
Sử dụng phương pháp tìm GTNN, GTLN của hàm số.
Cách giải:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
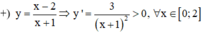
![]()
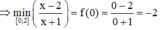
![]()
![]()
![]()
Cho hàm số f(x)liên tục trên đoạn [-2;3] có đồ thị như hình vẽ dưới đây. Gọi m, Mlần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số trên đoạn [-2;3]. Giá trị của 2m - 3M bằng:
A. -13
B. -16
C. -18
D. -15
Chọn B
Dựa vào đồ thị ta xác định được m = -3; M = 4. Ta có: 2m - 3M = -6 - 12 = -18.
Gọi M là giá trị lớn nhất của hàm số y = x 3 - 3 x 2 + x + m xét trên đoạn [2;4], m 0 là giá trị của tham số m để M đạt giá trị nhỏ nhất. Mệnh đề nào sau đây đúng.
A. 1 < m 0 < 5
B. - 7 < m 0 < - 5
C. - 4 < m 0 < 0
D. m 0 < - 8
Gọi M là giá trị lớn nhất của hàm số y = x 3 - 3 x 2 + x + m xét trên đoạn [2;4], m0 là giá trị của tham số m để M đạt giá trị nhỏ nhất. Mệnh đề nào sau đây đúng.
A. 1 < m 0 < 5
B. -7 < m 0 < -5
C. -4 < m 0 < 0
D. m 0 < -8
Chọn D.
Xét hàm số ![]() hàm số liên tục trên R
hàm số liên tục trên R
Có ![]()
![]()
![]() đồng biến trên [2;4]
đồng biến trên [2;4]
![]()
Nên ![]()
Do đó ![]()
![]()
Ta có ![]()
![]()
![]()
Dấu bằng xảy ra 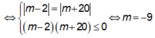
Vậy ![]()
![]()
Cho hàm số y = x + m x + 1 trên đoạn [1;2] giá trị lớn nhất và giá trị nhỏ nhất của hàm số thỏa mãn m a x [ 1 ; 2 ] y + m i n [ 1 ; 2 ] y = 16 3 Mệnh đề nào dưới đây đúng?
A. 0 < m ≤ 2
B. 2 < m ≤ 4
C. m ≤ 0
D. m > 4
Đáp án D
Ta có m a x [ 1 ; 2 ] y + m i n [ 1 ; 2 ] y = y ( 1 ) + y 2 = m + 1 2 + m + 2 3 = 16 3 ⇒ 5 m + 7 6 = 16 3
⇔
5
m
+
7
=
32
⇒
m
=
5