Hàm số nào dưới đây đồng biến trên R
A. y = x - 1 x + 2
B. y = x 3 + 4 x 2 + 3 x - 1
C. y = x 4 - 2 x 2 - 1
D. y = 1 3 x 3 - 1 2 x 2 + 3 x + 1
Những câu hỏi liên quan
Cho hàm số
y
f
(
x
)
liên tục trên R và có đạo hàm
f
(
x
)
(
1
-
x
)
2
(
x
+
1
)
3
(
3
-
x
)
. Hàm số
y
f
(
x
)
đồng biến trên khoảng nào dưới đây
Đọc tiếp
Cho hàm số y = f ( x ) liên tục trên R và có đạo hàm f ' ( x ) = ( 1 - x ) 2 ( x + 1 ) 3 ( 3 - x ) . Hàm số y = f ( x ) đồng biến trên khoảng nào dưới đây
Cho hàm số y f(x) xác định trên R, có bảng biến thiên sauHàm số y f(x) đồng biến trên khoảng nào dưới đây? A. (0;2) B. (-1;3) C. (-
∞
;3) D. (-
∞
;0)
Đọc tiếp
Cho hàm số y = f(x) xác định trên R, có bảng biến thiên sau
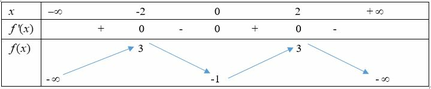
Hàm số y = f(x) đồng biến trên khoảng nào dưới đây?
A. (0;2)
B. (-1;3)
C. (- ∞ ;3)
D. (- ∞ ;0)
Cho hàm số f(x) có
f
(
x
)
x
2
-
2
x
,
∀
x
∈
R
. Hàm số
y
f
(
1
-
x
2
)
+
4
x
đồng biến trên khoảng nào dưới đây ? A.
-
6
;...
Đọc tiếp
Cho hàm số f(x) có f ' ( x ) = x 2 - 2 x , ∀ x ∈ R . Hàm số y = f ( 1 - x 2 ) + 4 x đồng biến trên khoảng nào dưới đây ?
A. - 6 ; 6
B. - ∞ ; 6
C. - 6 2 ; 6 2
D. - 6 2 ; + ∞
Cho hàm số yf(x) có đạo hàm trên R và đồ thị hàm số yf(x) như hình vẽ bên. Hàm số
g
(
x
)
2
f
(
1
-
x
)
+
1
3
x
3
-
4
x
-
1
đồng biến trên khoảng nào dưới đây
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm trên R và đồ thị hàm số y=f'(x) như hình vẽ bên. Hàm số g ( x ) = 2 f ( 1 - x ) + 1 3 x 3 - 4 x - 1 đồng biến trên khoảng nào dưới đây
Cho hàm số y f(x) liên tục trên R và có
f
(
x
)
x
+
1
2
x
-
1
3
2
-
x
. Hàm số y f(x) đồng biến trên...
Đọc tiếp
Cho hàm số y = f(x) liên tục trên R và có f ' ( x ) = x + 1 2 x - 1 3 2 - x . Hàm số y = f(x) đồng biến trên khoảng nào dưới đây?
A. 
.
B. 
.
C. 
.
D. 
.
Cho hàm số
y
f
x
liên tục trên R và có
f
x
x
+
1
2
x
−
1
3
2
−
x
. Hàm số
y
f...
Đọc tiếp
Cho hàm số y = f x liên tục trên R và có f ' x = x + 1 2 x − 1 3 2 − x . Hàm số y = f x đồng biến trên khoảng nào dưới đây?
A. (1;2)
B. − ∞ ; − 1
C. (-1;1)
D. 2 ; + ∞
Cho hàm số y=f(x) có đạo hàm liên tục trên R và có bảng biến thiên như hình bên dưới. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A. (1;+∞)
B.(-1;0)
C. (-∞;1)
D.(0;1)
Chọn đáp án D
Phương pháp
Sử dụng cách đọc bảng biến thiên để suy ra khoảng đồng biến của hàm số.
Hàm số liên tục trên (a;b) có y’>0 với x thuộc (a;b) thì hàm số đồng biến trên (a;b).
Cách giải
Từ BBT ta có hàm số đồng biến trên các khoảng (-∞;-1) và (0;1).
Đúng 0
Bình luận (0)
Cho hàm số y f(x) có đạo hàm trên R và có đồ thị hàm số y f(x) như hình bên. Hàm số y f (3-x) đồng biến trên khoảng nào dưới đây? A. B. C. D.
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm trên R và có đồ thị hàm số y = f'(x) như hình bên. Hàm số y= f (3-x) đồng biến trên khoảng nào dưới đây?
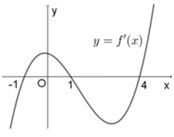
A. 
B. 
C. 
D. 
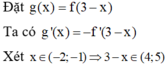
=> hàm số y=g(x) nghịch biến trên (-2; -1)
=>hàm số y=g(x) đồng biến trên (-1;2)
Chọn B
Đúng 0
Bình luận (0)
Cho hàm số y f(x) có đạo hàm trên R và có đồ thị hàm số yf(x) như hình bên. Hàm số yf(3-x) đồng biến trên khoảng nào dưới đây?
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm trên R và có đồ thị hàm số y=f'(x) như hình bên. Hàm số y=f(3-x) đồng biến trên khoảng nào dưới đây?
Cho hàm số
y
f
(
x
)
có đạo hàm
f
(
x
)
x
2
-
2
x
với mọi
x
∈
R
. Hàm số
g
(
x
)
f
2
-
x
2
+
1
-
x
2
+...
Đọc tiếp
Cho hàm số y = f ( x ) có đạo hàm f ' ( x ) = x 2 - 2 x với mọi x ∈ R . Hàm số g ( x ) = f 2 - x 2 + 1 - x 2 + 1 - 3 đồng biến trên các khoảng nào dưới đây?
