Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên bằng 2 a . Độ lớn của góc giữa đường thẳng SA và mặt phẳng đáy bằng:
A. 45 °
B. 75 °
C. 30 °
D. 60 °
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và góc giữa cạnh bên với mặt phẳng đáy bằng ∝
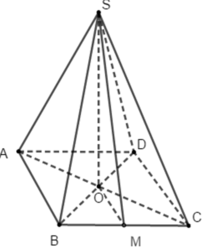
Tan của góc giữa mặt bên và mặt đáy bằng:
A. tan α
B. c o t α
C. 2 tan α
D. 2 2 tan α
Chân đường cao hình chóp đều S.ABCD trùng với tâm O của đáy ABCD. AO là hình chiếu của SA lên (ABCD)
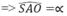
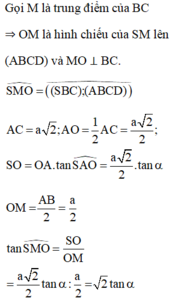
Đáp án C
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy, góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng 45° và SC = 2a. Tính thể tích V của khối chóp S.ABCD.

Vì SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD).
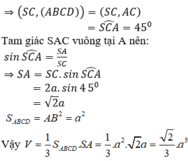
Cho hình chóp tứ giác đều S.ABCD cạnh đáy bằng cạnh bên bằng a. Góc giữa cạnh bên và mặt phẳng đáy bằng:
A. 60 o
B. 30 o
C. 45 o
D. không phải các kết quả A, B, C
Gọi O là giao điểm của AC và BD.
Vì S, ABCD là hình chóp tứ giác đều nên
Hình chiếu vuông góc của điểm S lên mp(ABCD) là điểm O nên góc giữa cạnh bên và mặt phẳng đáy là góc SBO.
Ta có: B D = a 2 ; B O = 1 2 B D = a 2
Lại có: S B 2 + S D 2 = B D 2 = 2 a 2 nên tam giác SBD vuông cân tại S. ⇒ S B O ^ = 45 0
Đáp án C
cho hình chóp S.ABCD có đáy là ABCD là hình vuông cạnh 5 cm, cạnh bên SA vuông góc với mặt phẳng đáy, góc giữa đường thẳng SB và mặt đáy bằng 45 độ. tính thể tích khối chóp S.ABCD
Lời giải:
$SA\perp (ABCD)$ nên $45^0=\angle (SB, (ABCD))=\angle (SB, AB)=\widehat{SBA}$
$\Rightarrow SA=AB=5$ (cm)
Thể tích khối chóp $S.ABCD$:
$V_{S.ABCD}=\frac{1}{3}.SA.S_{ABCD}=\frac{1}{3}.5.5^2=\frac{125}{3}$ (cm3)
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên tạo với đáy góc 60 ° .
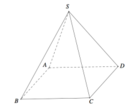
Khoảng cách giữa hai đường thẳng SA và BC bằng
A. 6 3 a
B. 10 5 a
C. 2 33 11 a
D. 42 7 a
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt phẳng đáy bằng 600. Tính thể tích khối chóp S.ABCD.
A. a 3 6
B. a 3 6 3
C. a 3 6 6
D. a 3 6 2
Đáp án C
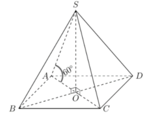
Gọi O là tâm đáy ABCD. Khi đó S O ⊥ A B C D
suy ra AO là hình chiếu vuông góc của SA lên mặt phẳng đáy. Khi đó góc giữa cạnh bên SA và đáy là S A O ^
Suy ra S A O ^ = 60 °
Vậy thể tích khối chóp là:
V = 1 3 . S O . S A B C D = a 3 6 6
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt phẳng đáy bằng 60 0 . Tính thể tích khối chóp S.ABCD.
A. a 3 6 2
B. a 3 6 6
C. a 3 6
D. a 3 6 3
Đáp án B
Ta có: 2 B I 2 = a 2 ⇒ B I = a 2 ; S I = B I tan 60 0 = a 3 2
Thể tích khối chóp S.ABCD là
V = 1 3 S I . S A B C D = 1 3 a 3 2 . a 2 = a 3 6 6
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt phẳng đáy bằng 60 0 . Tính thể tích khối chóp S.ABCD
A. a 3 6 2
B. a 3 6 6
C. a 3 6
D. a 3 6 3
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình chữ nhật, cạnh A B = a , A D = 2 a , cạnh bên SA vuông góc với mặt phẳng đáy, góc giữa cạnh SD và mặt phẳng đáy bằng 60 o . Thể tích V của khối chóp S.ABCD là
A. V = 2 a 3 3 .
B. V = 4 a 3 3 .
C. V = a 3 3 .
D. V = 4 a 3 3 .