Hỏi mệnh đề nào dưới đây là sai
A. ( ∫ f ( x ) d x ) ' = f ( x )
B. ∫ k f ( x ) d x = k ∫ f ( x ) d x
C. ∫ [ f ( x ) + g ( x ) ] d x = ∫ f ( x ) d x + ∫ g ( x ) d x
D. ∫ [ f ( x ) . g ( x ) ] d x = ∫ f ( x ) d x . ∫ g ( x ) d x
Những câu hỏi liên quan
Cho hàm số y f(x) liên tục trên [a;b]. Mệnh đề nào dưới đây sai?
Đọc tiếp
Cho hàm số y = f(x) liên tục trên [a;b]. Mệnh đề nào dưới đây sai?
Cho hàm số F(x) là một nguyên hàm của hàm số f(x) xác định trên K. Mệnh đề nào dưới đây sai? A.
x
∫
f
x
d
x
f
x
B.
∫
f
x
d...
Đọc tiếp
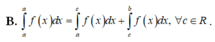
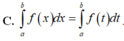
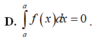
Cho hàm số F(x) là một nguyên hàm của hàm số f(x) xác định trên K. Mệnh đề nào dưới đây sai?
A. x ∫ f x d x ' = f ' x
B. ∫ f x d x ' = f x
C. ∫ f x d x ' = F ' x
D. ∫ f x d x = F x + C
Cho hàm số F(x) là một nguyên hàm của hàm số f(x) xác định trên K. Mệnh đề nào dưới đây sai?
Đọc tiếp
Cho hàm số F(x) là một nguyên hàm của hàm số f(x) xác định trên K. Mệnh đề nào dưới đây sai?
Cho hàm số y f(x) liên tục trên đoạn [a; b]. Mệnh đề nào dưới đây sai?
Đọc tiếp
Cho hàm số y = f(x) liên tục trên đoạn [a; b]. Mệnh đề nào dưới đây sai?
Cho hàm số yf(x) liên tục trên đoạn [a;b]. Mệnh đề nào dưới đây sai?
Đọc tiếp
Cho hàm số y=f(x) liên tục trên đoạn [a;b]. Mệnh đề nào dưới đây sai?
Cho hàm số y f(x) liên tục trên đoạn [a;b]. Mệnh đề nào dưới đây sai?
Đọc tiếp
Cho hàm số y = f(x) liên tục trên đoạn [a;b]. Mệnh đề nào dưới đây sai?
Cho hàm số yf(x) liên tục trên đoạn [a;b]. Mệnh đề nào dưới đây sai? A.
∫
a
b
f
x
d
x
∫
a
b
f
t
d
t
B.
∫
a
b
f
x
d
x...
Đọc tiếp
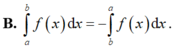
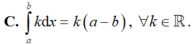
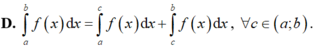
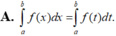
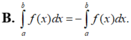
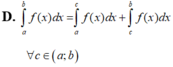
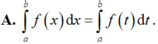
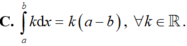
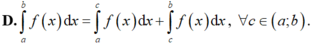
Cho hàm số y=f(x) liên tục trên đoạn [a;b]. Mệnh đề nào dưới đây sai?
A. ∫ a b f x d x = ∫ a b f t d t
B. ∫ a b f x d x = - ∫ a b f x d x
C. ∫ a b k d x = k a - b , ∀ k ∈ ℝ
D. ∫ a b f x d x = ∫ a c f x d x + ∫ c b f x d x , ∀ c ∈ a ; b
Cho hàm số f (x) có bảng biến thiên dưới đây. Mệnh đề nào sau đây là sai? A. Hàm số nghịch biến trên khoảng (-∞; -1) B. Hàm số nghịch biến trên khoảng (0;1) C. Hàm số đồng biến trên khoảng (0;+∞) D. Hàm số đồng biến trên khoảng (1;+∞)
Đọc tiếp
Cho hàm số f (x) có bảng biến thiên dưới đây. Mệnh đề nào sau đây là sai?
A. Hàm số nghịch biến trên khoảng (-∞; -1)
B. Hàm số nghịch biến trên khoảng (0;1)
C. Hàm số đồng biến trên khoảng (0;+∞)
D. Hàm số đồng biến trên khoảng (1;+∞)
Chọn C.
Phương pháp: Câu hỏi về sự biến thiên nên ta quan sát chiều mũi tên và đưa rakết luận.
Cách giải: Dễ thấy mệnh đề C sai vì trên khoảng 0 ; + ∞ hàm số nghịch biến trên (0;1) và đồng biến trên 1 ; + ∞ .
Đúng 0
Bình luận (0)
Cho hàm số f (x) có bảng biến thiên dưới đây. Mệnh đề nào sau đây là sai? A. Hàm số nghịch biến trên khoảng (-∞; -1) B. Hàm số nghịch biến trên khoảng (0;1) C. Hàm số đồng biến trên khoảng (0+;∞) D. Hàm số đồng biến trên khoảng (1;+∞)
Đọc tiếp
Cho hàm số f (x) có bảng biến thiên dưới đây. Mệnh đề nào sau đây là sai?
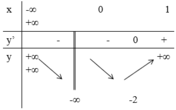
A. Hàm số nghịch biến trên khoảng (-∞; -1)
B. Hàm số nghịch biến trên khoảng (0;1)
C. Hàm số đồng biến trên khoảng (0+;∞)
D. Hàm số đồng biến trên khoảng (1;+∞)
Cho hàm số
f
(
x
)
a
x
4
+
b
x
3
+
c
x
3
+
d
x
+
e
(
a
≠
0
)
. Biết rằng hàm số f(x) có đạo hàm là f’(x) và hàm số yf’(x) có đồ thị như hình vẽ dưới. Khi đó mệnh đề nào sau đây sai? A. Hàm số f(x) nghịch biến trên khoảng (-1;1...
Đọc tiếp
Cho hàm số f ( x ) = a x 4 + b x 3 + c x 3 + d x + e ( a ≠ 0 ) . Biết rằng hàm số f(x) có đạo hàm là f’(x) và hàm số y=f’(x) có đồ thị như hình vẽ dưới. Khi đó mệnh đề nào sau đây sai?
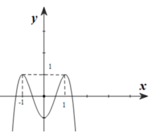
A. Hàm số f(x) nghịch biến trên khoảng (-1;1)
B. Hàm số f(x) đồng biến trên khoảng (0;+∞)
C. Hàm số f(x) đồng biến trên khoảng (-2;1)
D. Hàm số f(x) nghịch biến trên khoảng (-∞;-2)
Chọn A
Phương pháp:
Nếu f ' ( x ) ≥ 0 , ∀ x ∈ a ; b và chỉ bằng 0 tại hữu hạn điểm trên đó thì f(x) đồng biến trên khoảng (a;b).
Nếu f ' ( x ) ≤ 0 , ∀ x ∈ a ; b và chỉ bằng 0 tại hữu hạn điểm trên đó thì f(x) nghịch biến trên khoảng (a;b) Cách giải:
Quan sát đồ thị hàm số y=f’(x) , ta thấy f’(x) >0 =>Hàm số f (x) đồng biến trên
khoảng (-1;1).
=>Mệnh đề ở câu A là sai.
Đúng 0
Bình luận (0)