Cho hình lập phương ABCD.A'B'C'D'. Mặt phẳng B C A ' D ' chia khối lập phương trên thành hai khối đa diện có tên là
A. lăng trụ đều
B. chóp tam giác đều.
C. lăng trụ đứng.
D. chóp tứ giác đều.
Những câu hỏi liên quan
Cho hình lập phương ABCD.ABCD. Mặt phẳng (BCAD) chia khối lập phương trên thành hai khối đa diện có tên là A. lăng trụ đều. B. chóp tam giác đều. C. lăng trụ đứng. D. chóp tứ giác đều.
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D'. Mặt phẳng (BCA'D') chia khối lập phương trên thành hai khối đa diện có tên là
A. lăng trụ đều.
B. chóp tam giác đều.
C. lăng trụ đứng.
D. chóp tứ giác đều.
Cho khối lập phương ABCD.A'B'C'D'. Mặt phẳng (BDD'B') chia khối lập phương thành
A. Hai khối lăng trụ tam giác.
B. Hai khối tứ diện.
C. Hai khối lăng trụ tứ giác.
D. Hai khối chóp tứ giác.
Cho khối lập phương ABCD.ABCD cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, AD. Mặt phẳng (MBDN) chia khối lập phương đã cho thành hai khối đa diện. Gọi (H) là khối đa diện chứa đỉnh A. Thể tích của khối đa diện (H) bằng:A.
a
3
9
B.
a
3
6
C.
a...
Đọc tiếp
Cho khối lập phương ABCD.A'B'C'D' cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, AD. Mặt phẳng (MB'D'N) chia khối lập phương đã cho thành hai khối đa diện. Gọi (H) là khối đa diện chứa đỉnh A. Thể tích của khối đa diện (H) bằng:
A. a 3 9 B. a 3 6
C. a 3 4 D. 7 a 3 24
Chọn D.
Dễ thấy A'A, B'M, D'N đồng quy tại S, SA' = 2a. Từ đó, ta tính được V S . A ' B ' D ' và V S . AMN . Suy ra tính được V H
Đúng 0
Bình luận (0)
Cho hình lập phương
A
B
C
D
.
A
B
C
D
.
Biết tích của khoảng cách từ điểm B và điểm D đến mặt phẳng (D’AC) bằng
6
a
2
a
0
.
Giả sử thể tích của khối lập phương
A
B
C
D
.
A
B
C...
Đọc tiếp
Cho hình lập phương A B C D . A ' B ' C ' D ' . Biết tích của khoảng cách từ điểm B' và điểm D đến mặt phẳng (D’AC) bằng 6 a 2 a > 0 . Giả sử thể tích của khối lập phương A B C D . A ' B ' C ' D ' là k a 3 . Chọn mệnh đề đúng trong các mệnh đề sau.
A. k ∈ 20 ; 30
B. k ∈ 100 ; 120
C. k ∈ 50 ; 80
D. k ∈ 40 ; 50
Cho hình lập phương ABCD.ABCD. Biết tích của khoảng cách từ điểm B và điểm D đến mặt phẳng (D’AC) bằng
6
a
2
a
0
. Giả sử thể tích của khối lập phương ABCD.ABCD là
k
a
3
. Chọn mệnh đề đúng trong các mệnh đề sau.
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D'. Biết tích của khoảng cách từ điểm B' và điểm D đến mặt phẳng (D’AC) bằng 6 a 2 a > 0 . Giả sử thể tích của khối lập phương ABCD.A'B'C'D' là k a 3 . Chọn mệnh đề đúng trong các mệnh đề sau.
Cho hình lập phương
A
B
C
D
.
A
B
C
D
cạnh a. Gọi M, N lần lượt là trung điểm của cạnh
A
B
và BC. Mặt phẳng (DMN) chia khối lập phương thành hai khối đa diện. Gọi (H) là khối đa diện chứa đỉnh A và
H
là khối đa diện còn lại. Tính tỉ số
V...
Đọc tiếp
Cho hình lập phương A B C D . A ' B ' C ' D ' cạnh a. Gọi M, N lần lượt là trung điểm của cạnh A ' B ' và BC. Mặt phẳng (DMN) chia khối lập phương thành hai khối đa diện. Gọi (H) là khối đa diện chứa đỉnh A và H ' là khối đa diện còn lại. Tính tỉ số V H V H '
A. V H V H ' = 55 89
B. V H V H ' = 37 48
C. V H V H ' = 1 2
D. V H V H ' = 2 3
Cho hình lập phương ABCD.ABCD, gọi M và N lần lượt là tâm của các hình vuông ABCD và ABCD. Mặt phẳng (AMN) chia khối lập phương thành hai phần có thể tích là
V
1
và
V
2
. Tính tỷ số
V
2
V
1
.
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D', gọi M và N lần lượt là tâm của các hình vuông ABCD và A'B'C'D'. Mặt phẳng (A'MN) chia khối lập phương thành hai phần có thể tích là V 1 và V 2 . Tính tỷ số V 2 V 1 .
Cho hình lập phương
A
B
C
D
.
A
B
C
D
, gọi
M
và
N
lần lượt là tâm của các hình vuông
A
B
C
D
và
D
C
C
D
. Mặt phẳng
A
M
N
chia khối lập phươn...
Đọc tiếp
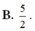
Cho hình lập phương A B C D . A ' B ' C ' D ' , gọi M và N lần lượt là tâm của các hình vuông A B C D và D C C ' D ' . Mặt phẳng A ' M N chia khối lập phương thành hai phần có thể tích là V 1 và V 2 V 1 < V 2 . Tính tỷ số V 2 V 1
A. 5 3
B. 5 2
C. 3 2
D. 2
Cho hình lập phương
A
B
C
D
.
A
B
C
D
có cạnh bằng a. Gọi M, N lần lượt nằm trên các cạnh
A
B
và BC sao cho
M
A
M
B
và NB 2NC. Mặt phẳng (DMN) chia khối lập phương đã cho thành hai khối đa diện...
Đọc tiếp
Cho hình lập phương A B C D . A ' B ' C ' D ' có cạnh bằng a. Gọi M, N lần lượt nằm trên các cạnh A ' B ' và BC sao cho M A ' = M B ' và NB = 2NC. Mặt phẳng (DMN) chia khối lập phương đã cho thành hai khối đa diện. Gọi V H là thể tích khối đa diện chứa đỉnh A, V ( H ' ) là thể tích khối đa diện còn lại. Tỉ số V H V H ' bằng
A. 151 209
B. 209 360
C. 2348 3277
D. 151 360
