Cho hàm số f ( x ) = ax + 3 b x 2 + c x + d ( a , b , c , d ∈ R ) có đồ thị như hình vẽ sau. Số nghiệm của phương trình 4f(x) + 3 = 0 là
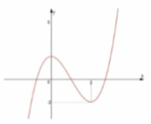
A. 3
B. 2
C. 1
D. 0
B1: Cho hàm số \(y=f\left(x\right)=x^2+ax-a+5\).Tìm a biết f(-2)=2004
B2: Cho hàm số \(y=f\left(x\right)=ax+b.\)Tìm và b biết f(1)=2 và f(2)=3
B3: Cho hàm số \(y=f\left(x\right)=ax^2+bx+c.\)Tìm a,b,c biết f(o)=1,f(1)=2,f(2)=3
B4:Cho hàm số y=x+1
a,tìm tọa độ điểm A, biết A là giao điểm đồ thị với trục tung
b, Tìm tọa độ điểm B biết B là giao điểm của đồ thị với trục hoành
B5: tìm tọa độ giao điểm của đồ thị hàm số y=2x và y=3x-1
B6: Cho hàm số y=ax^2+bx+c tìm a,b,c biết đồ thị hàm số đi qua điểm A(0,1), B(1,2), C(-1,0)
HELP ME!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
a) Cho hàm số y = f(x) = ax - 3. Tìm a biết f(2) = 5.
b) Cho hàm số y = f(x) = ax + b. Tìm a và b biết f(0) = 3 và f(1) = 4
a ) Ta có : f(2) = 5
\(\Leftrightarrow\hept{\begin{cases}f\left(x\right)=f\left(2\right)\\\text{ax}-3=5\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=2\\a.2-3=5\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=2\\a=4\end{cases}}\)
Vậy a = 4
b ) Ta có : f(0) = 3
\(\Leftrightarrow\hept{\begin{cases}f\left(x\right)=f\left(0\right)\\\text{ax}+b=3\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=0\\a.0+b=3\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=0\\b=3\end{cases}}\) ( 1 )
Ta có : f ( 1 ) = 4
\(\Leftrightarrow\hept{\begin{cases}f\left(x\right)=f\left(1\right)\\\text{ax}+b=4\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=1\\a.1+b=4\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=1\\a+b=4\end{cases}}\) ( 2 )
Thay b = 3 ở ( 1 ) vào a+b=4 ở ( 2 ) ta được : a + 3 = 4
a = 1
Vậy a = 1 ; b = 3
a)Cho hàm số f(x)=ax^2+bx+c là các số hữu thỉ .Chứng tỏ rằng f(-2),f(3)lớn hơn hoặc bằng 0 biết rằng 13a+b+2c=0
b)Cho hàm số f(x) xác định với mọi x thuộc R .Biết rằng với mọi x ta đều có f(x)+3*f(1/x)=x^2
a) Cho hàm số y=f(x)=ax5+bx3+cx-5 (a,b,c thuộc R)
Cho f(-3)=208. Tính f(3)=?
b) Cho hàm số y=g(x)=ax4-bx2+x+3 (a,b thuộc R)
Cho g(2)=17. Tính g(-2)=?
cho hàm số y=f(x)=ax^2+bx+c. tìm a,b,c biết : f(0)=3; f(1)=0; f(3)=0
LÀM XONG NHỚ T.I.C.K Á
F(0)=3 =>C=3
F(1)=0=>A+B+C=0=>A+B= -3 (1)
F(-1)=1=>A+B+C=1=>A-B= -2 (2)
KẾT HỢP 1 VÀ 2 =>A=5/2;B=1/2
a)xác định a để nghiệm của đa thức f x = ax - 4 Cũng là nghiệm của đa thức g(x) = x^2 trừ x = 2 .
b)cho f(x) = ax^3 = bx^2 = cx = d trong đó A,B,C,D là hàm số và thỏa mãn b + 3 a + c. chứng tỏ rằng F(1) = F (-2)
cho hàm số y=f(x)=ax^2+bx+c.Tim a,b,c biết f(-2)=0;f(2)=0 và a-c=3
Ta có: \(y=f\left(x\right)=ax^{2\:}+bx+c\)
\(\Rightarrow f\left(-2\right)=4a-2b+c=2a-2b+2a+c=2a-2b+3c+6=0\)
\(\Rightarrow2a-2b+3c=-6\left(1\right)\)
\(f\left(2\right)=4a+2b+c=2a+2b+2a+c=2a+2b+3c+6=0\)
\(\Rightarrow2a+2b+3c=-6\left(2\right)\)
Từ (1)(2) \(\Rightarrow2a-2b+3c=2a+2b+3c\)
\(\Rightarrow2a-2b+3c-\left(2a+2b+3c\right)=0\)
\(\Rightarrow2a-2b+3c-2a-2b-3c=0\)
\(\Rightarrow\left(2a-2a\right)-\left(2b+2b\right)+\left(3c-3c\right)=0\)
\(\Rightarrow-4b=0\)
\(\Rightarrow b=0\)
\(\Rightarrow2a+3c=-6\)
\(\Rightarrow5c+6=-6\)
\(\Rightarrow5c=-12\)
\(\Rightarrow c=\frac{-12}{5}\)
\(\Rightarrow a=\frac{-12}{5}+3=\frac{3}{5}\)
Vậy \(a=\frac{3}{5};c=\frac{-12}{5};b=0\)
Cho hàm số y= f(x)= ax^2+bx+c
Tìm a,b,c nếu biết f(0)=2; f(2)=3; f(3)=4.
Cho hàm số y=f(x)=x^3+ax^2+bx+4 có đồ thị (C) như hình vẽ. Hỏi (C) là đồ thị của hàm số y=f(x) nào?
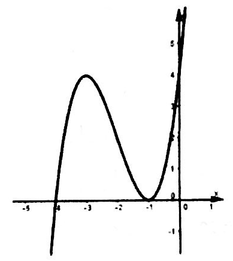
A. y = f ( x ) = x 3 - 3 x 2 + 4
B. y = f ( x ) = x 3 + 6 x 2 + 9 x + 4
C. y = f ( x ) = x 3 + 3 x 2 + 4
D. y = f ( x ) = x 3 - 6 x 2 + 9 x + 4
Cho hàm số f(x)=ax^2+bx+c(a,b,c nguyên)
CMR nếu f(x) chia hết cho 3 vs mọi giá trị của x thì a,b,c đều chia hết cho 3.
Ta có f (x) = ax2 + bx + c chia hết cho 3 với mọi gt của x
Nếu x = 0 => c \(⋮\)3
Nếu x = 1 => a + b + c \(⋮\)3 => a + b \(⋮\)3 => \(\hept{\begin{cases}a⋮3\\b⋮3\end{cases}}\)
Vậy ...