\(A^2=x^2+\dfrac{v^2}{\omega^2}\Leftrightarrow16=x^2+\dfrac{\left(20\sqrt{2}\right)^2.10}{10^2.10}\Rightarrow x=\pm2\sqrt{2}\left(cm\right)=\pm\dfrac{\sqrt{2}}{2}A\)

\(\Rightarrow\varphi=\dfrac{\pi}{4}+\dfrac{\pi}{2}\Rightarrow t=\dfrac{3\pi}{4.10\pi}=0,075\left(s\right)\)

 Từ pt \(v=16\pi\cos\left(4\pi t-\dfrac{\pi}{6}\right)=16\pi\cos\left(4\pi t-\dfrac{2\pi}{3}+\dfrac{\pi}{2}\right)\) (cm/s), ta suy ra \(\omega=4\pi\left(rad/s\right)\), lại có \(\omega A=16\pi\Leftrightarrow A=\dfrac{16\pi}{\omega}=4\left(cm\right)\)

 \(\varphi_0=-\dfrac{2\pi}{3}\); \(T=\dfrac{2\pi}{\omega}=0,5\left(s\right)\)

 Đường tròn lượng giác: 

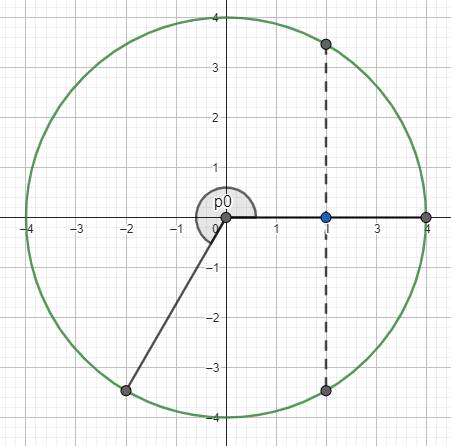
 Từ đây, ta có thể thấy tại thời điểm lần thứ 2023 vật chuyển động qua vị trí \(x=2\) kể từ khi dao động, góc quét của vật là \(\Delta\varphi=\dfrac{\pi}{3}+1011.2\pi=\dfrac{6067}{3}\pi\) (rad)

 Thời điểm lần thứ 2023 vật chuyển động qua vị trí \(x=2\) kể từ lúc bắt đầu dao động là \(\Delta t=\dfrac{\Delta\varphi}{2\pi}.T=\dfrac{\dfrac{6067}{3}\pi}{2\pi}.0,5=\dfrac{6067}{12}\approx505,58\left(s\right)\)

Đáp án C

Phương pháp: Áp dụng công thức tính vận tốc cực đại của vật dao động điều hoà  v max = Aω

Vận tốc cực đại mà vật đạt được trong quá trình dao động là v max = Aω = 2 π . 4 = 8 π

Đáp án A

Phương pháp: a = - ω²x

Cách giải:

x (t=0,25s) = 1cm => a = - ω²x = - 40cm/s²

Chọn đáp án D

Tốc độ trung bình trong một chu kì:

v ¯ = S △ t = 4 A T = 4. A ω 2 π = 4.5.2 π 2 π = 20 ( c m / s ) .