Tìm m để hệ bất phương trình sau vô nghiệm
3 x + 5 ≥ x - 1 x + 2 2 ≤ x - 1 2 + 9 mx + 1 > m - 2 x + m
A. m > 3
B. m ≥ 3
C. m < 2
D. Tất cả sai
Những câu hỏi liên quan
Tìm m để hệ bất phương trình sau vô nghiệm
3
x
+
4
x
+
9
1
-
2
x
≤...
Đọc tiếp
Tìm m để hệ bất phương trình sau vô nghiệm
3 x + 4 > x + 9 1 - 2 x ≤ m - 3 x + 1
A. m < 1/2
B. m< 5/2
C. m ≤ 3/2
D. m ≤ 5/2
Chọn D
+ Xét bpt : 3x-4> x+ 9 hay x> 5/ 2
Suy ra tập nghiệm của bpt đầu là : S1= ( 5/2; + ∞)
+ Xét bpt: 1-2x ≤ m-3x+ 1
Hay x ≤ m
Suy ra tập nghiệm của bpt thứ 2 là S2= ( -∞; m]
Để hệ bpt vô nghiệm khi và chỉ khi :
Đúng 0
Bình luận (0)
Giúp mình 2 câu này với ạ:
1. Tìm m để bất phương trình sau có nghiệm đúng với mọi x :
mx2 +(m+1)x+m-1 <0
2. Tìm m để bất phương trình sau vô nghiệm :
mx2-4(m+1)x+m-5<0
1.
\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\\Delta=\left(m+1\right)^2-4m\left(m-1\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\-3m^2+7m+1< 0\end{matrix}\right.\)
\(\Leftrightarrow m< \dfrac{7-\sqrt{61}}{6}\)
2.
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\\Delta'=4\left(m+1\right)^2-m\left(m-5\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\3m^2+13m+4\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\-4\le m\le-\dfrac{1}{3}\end{matrix}\right.\)
Không tồn tại m thỏa mãn
Đúng 4
Bình luận (3)
Tìm tất cả các giá trị thực của tham số m để hệ bất phương trình
x
-
3
0
m
-
x
...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hệ bất phương trình x - 3 < 0 m - x < 1 vô nghiệm.
A. m < 4
B. m > 4
C. m ≤ 4
D. m ≥ 4
Chọn D
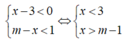
Hệ bất phương trình vô nghiệm khi và chỉ khi m - 1 ≥ 3 hay m ≥ 4
Đúng 0
Bình luận (0)
Tìm m để hệ bất phương trình vô nghiệm \(\left\{{}\begin{matrix}mx\le m-3\\\left(m+3\right)x\ge m-9\end{matrix}\right.\)
tìm m để hệ bất phương trình \(\left\{{}\begin{matrix}\left(3-x\right)\left(4-x\right)lớnhơn0\\x< m-1\end{matrix}\right.\) vô nghiệm
\(\left\{{}\begin{matrix}\left(3-x\right)\left(4-x\right)>0\\x< m-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x< 3\\x>4\end{matrix}\right.\\x< m-1\end{matrix}\right.\)
Đặt \(A=\left(-\infty;3\right)\cup\left(4;+\infty\right)\)
B = \(\left(-\infty;m-1\right)\)
Để hệ bất phương trình vô nghiệm thì A \(\cap\) B = ∅
⇒ m ∈ ∅
Vậy không có giá trị của m thỏa mãn ycbt
Đúng 1
Bình luận (0)
1. Định m để bất phương trình m(x-1) > 2mx - 3 có vô số nghiệm
2. Tìm m để m(x-2) + m -1 < 0 bất phương trình có vô số nghiệm
Cho hệ phương trình x 2y=5 (1)
mx y=4 (2)
a) Tìm m để hệ phương trình vô nghiệm
b) Tìm m để hệ có nghiệp duy nhất
c) Tìm m để hệ vô số nghiệm
Tìm giá trị m để bất phương trình sau VÔ NGHIỆM
m2x - 3 < x + m2 - 4m
(x là ẩn số, m là hệ số bằng chữ)
Ta có \(bpt\Leftrightarrow m^2x-x< m^2-4m+3\Leftrightarrow\left(m^2-1\right)x< m^2-4m+3\)
\(\Leftrightarrow\left(m-1\right)\left(m+1\right)x< \left(m-1\right)\left(m+3\right)\)
\(\Leftrightarrow\left(m-1\right)\left[\left(m+1\right)x-m-3\right]< 0\)
Với m = 1, bpt vô nghiệm
Với m > 1, \(bpt\Leftrightarrow\left(m+1\right)x-\left(m+3\right)< 0\)
Khi đó bpt có nghiệm \(x< \frac{m+3}{m+1}\)
Với m < 1, \(bpt\Leftrightarrow\left(m+1\right)x-\left(m+3\right)>0\)
Khi đó bpt cũng luôn có nghiệm.
Vậy bpt vô nghiệm khi m = 1.
Đúng 0
Bình luận (0)
Tìm m để các hệ bất phương trình sau : có nghiệm, vô nghiệm, có nghiệm duy nhất ( Làm cả 3 cái đó trong 1 hệ chứ không phải là chỉ làm 1 cái trong 1 hệ thôi đâu ! )a) left{{}begin{matrix}x+m-103m-2-x0end{matrix}right. b) left{{}begin{matrix}x-10mx-30end{matrix}right. c) left{{}begin{matrix}x+4m^2le2mx+13x+22x-1end{matrix}right.d) left{{}begin{matrix}7x-2ge-4x+192x-3m+2 0end{matrix}right. e) left{{}begin{matrix}mx-10left(3m-2right)x-m0end{matrix}right.
Đọc tiếp
Tìm m để các hệ bất phương trình sau : có nghiệm, vô nghiệm, có nghiệm duy nhất ( Làm cả 3 cái đó trong 1 hệ chứ không phải là chỉ làm 1 cái trong 1 hệ thôi đâu ! )
a) \(\left\{{}\begin{matrix}x+m-1>0\\3m-2-x>0\end{matrix}\right.\) b) \(\left\{{}\begin{matrix}x-1>0\\mx-3>0\end{matrix}\right.\) c) \(\left\{{}\begin{matrix}x+4m^2\le2mx+1\\3x+2>2x-1\end{matrix}\right.\)
d) \(\left\{{}\begin{matrix}7x-2\ge-4x+19\\2x-3m+2< 0\end{matrix}\right.\) e) \(\left\{{}\begin{matrix}mx-1>0\\\left(3m-2\right)x-m>0\end{matrix}\right.\)