Biết số phức z thỏa mãn: (2-z) i + z ¯ ∈ ℝ thì tập hợp điểm biểu diễn số phức z là:
A. Một đường tròn.
B. Một Parabol.
C. Một Elip.
D. Một đường thẳng.
Trong mặt phẳng tọa độ, tập hợp các điểm M x ; y biểu diễn của số phức z = x + y i x ; y ∈ ℝ thỏa mãn z + 1 + 3 i = z - 2 - i là
A. Đường tròn tâm O bán kính R = 1
B. Đường tròn đường kính AB với A - 1 ; - 3 và B 2 ; 1
C. Đường trung trực của đoạn thẳng AB với A - 1 ; - 3 và B 2 ; 1
D. Đường thẳng vuông góc với đoạn AB tại A với A A - 1 ; - 3 , B 2 ; 1
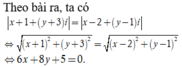
Phương trình đường trung trực của AB là: 6x + 8y + 5 = 0
Vậy tập hợp các điểm M(x;y) biểu diễn số phức z và thỏa mãn yêu cầu bài toán là đường thẳng trung trực của đoạn AB với A - 1 ; - 3 và B 2 ; 1
Chọn C.
Xác định tập hợp các điểm trong mặt phẳng phức biểu diễn số phức z = x + i y , x , y ∈ ℝ thỏa mãn điều kiện z = 2 .
A. Đường tròn x 2 + y 2 = 4 .
B. Đường thẳng x = 2 .
C. Đường thẳng y = 2
D. Hợp hai đường thẳng x = 2, y = 2 .
Đáp án A
z = 2 ⇔ x 2 + y 2 = 2 ⇔ x 2 + y 2 = 4 .
Gọi M là điểm biểu diễn cho số phức z =x +yi(x,y ϵ ℝ) thỏa mãn |z +1 -2i|=|z|. Tập hợp điểm là đường thẳng nào sau đây?
A. 2x +4y +5 =0.
B. 2x -4y +5 =0.
C. 2x -4y +3 =0.
D. x -2y +1= 0
Cho hai số phức w và z thỏa mãn w - 1 + 2 i = z . Biết tập hợp các điểm biểu diễn của số phức z là đường tròn tâm I(-2;3) bán kính r = 3. Tìm tập hợp các điểm biểu diễn của số phức
A. Là một đường thẳng song song trục tung
B. Là một đường thẳng không song song với trục tung
C. Là đường tròn, tọa độ tâm (-3;5) bán kính bằng 3 5
D. Là đường tròn, tọa độ tâm (-1;1) bán kính bằng 3
Ta có : w - 1 + 2 i = z ⇔ w = z + 1 - 2 i . Suy ra quỹ tích các điểm biểu diễn số phức w có được từ quỹ tích các điểm biểu diễn số phức z bằng cách thực hiện phép tịnh tiến theo v → = ( 1 ; - 2 ) . Do đó quỹ tích quỹ tích các điểm biểu diễn số phức w là đường tròn tâm (-1;1) bán kính bằng 3.
Đáp án D
Tập hợp các điểm trong mặt phẳng phức biểu diễn các số phức z thỏa mãn 2|z-i|=|z- z +2i| là:
A. Đường tròn tâm I(0;1), bán kính R = 1
B. Đường tròn tâm I( 3 ;0), bán kính R = 3
C. Parabol y = x 2 4
D. Parabol x = y 2 4
Tập hợp điểm biểu diễn số phức z thỏa mãn z + i − 2 = 3 là
A. Đường tròn tâm I 2 ; − 1 bán kính R = 3
B. Đường tròn tâm I 2 ; − 1 bán kính R = 9
C. Đường tròn tâm I − 2 ; 1 bán kính R = 9
D. Đường tròn tâm I − 2 ; 1 bán kính R = 3
Tìm tập hợp điểm biểu diễn số phức z thỏa mãn z + 2 - i = 3
A. Đường tròn tâm I(2;-1) bán kính R = 1
B. Đường tròn tâm I(-2;1) bán kính R = 3
C. Đường tròn tâm I(1;-2) bán kính R = 3
D. Đường tròn tâm I(-2;1) bán kính R = 3
Tìm tập hợp điểm biểu diễn số phức z thỏa mãn |z+2-i|=3
A. Đường tròn tâm I(2;-1), bán kính R= 1
B. Đường tròn tâm I(-2;l), bán kính R= 3
C. Đường tròn tâm I(1 ;-2), bán kính R= 3
D. Đường tròn tâm I(-2;l), bán kính R= 3
Tìm tập hợp điểm biểu diễn số phức z thỏa mãn |z+2-i| = 3
A. Đường tròn tâm I(2;-1) bán kính R = 1
B. Đường tròn tâm I(-2;1) bán kính R = 3
C. Đường tròn tâm I(1;-2) bán kính R = 3
D. Đường tròn tâm I(-2;1) bán kính R = 3
Đáp án D
Đặt ![]() khi đó
khi đó ![]()
![]()
Do đó tập hợp điểm biễu diễn z là đường tròn tâm I(-2;1) bán kính R = 3