Giá trị của I = ∫ a b 2 x d x được tính là:
![]()
![]()
![]()
![]()
a) Rút gọn A và tìm điều kiện của x để giá trị của A được xác định. b) Tính giá trị của A tại x = -2. c) Tính giá trị của x để giá trị của A = 4. d) Tính giá trị của x để giá trị của A = 1
a) ĐKXĐ: x≠ \(\dfrac{1}{2}\); x≠ \(\dfrac{-1}{2}\); x≠0
A= \(\left(\dfrac{1}{2x-1}+\dfrac{3}{1-4x^2}-\dfrac{2}{2x+1}\right):\dfrac{x^2}{2x^2+x}\)
= \(\left(\dfrac{2x+1-3-2\left(2x-1\right)}{4x^2-1}\right):\dfrac{x^2}{2x^2+x}\)
= \(\left(\dfrac{2x+1-3-4x+2}{4x^2-1}\right):\dfrac{x^2}{2x^2+x}\)
= \(\dfrac{-4x}{\left(2x+1\right)\left(2x-1\right)}.\dfrac{x\left(2x+1\right)}{x^2}\)
= \(\dfrac{-4x^2}{x^2\left(2x-1\right)}\)
= \(\dfrac{-4}{2x-1}\)
b) Tại x= -2 ta có A= \(\dfrac{-4}{2.\left(-2\right)-1}\)= \(\dfrac{4}{5}\)
c) A= 4 ta có \(\dfrac{-4}{2x-1}\)=4
⇔ -4 = 4(2x-1)
⇔ -4 = 8x-4
⇔ x = 0
d) A=1 ta có \(\dfrac{-4}{2x-1}\)=1
⇔ -4 = 2x-1
⇔ x= \(\dfrac{-3}{2}\)
Tính rồi viết vào chỗ chấm thích hợp:
a) 10 x 2 x 3 = ....................
Giá trị của biểu thức 10 x 2 x 3 là ...........
b) 6 x 3 : 2 = ....................
Giá trị của biểu thức 6 x 3 : 2 là ...........
c) 84 : 2 : 2 = ....................
Giá trị của biểu thức 84 : 2 : 2 là ...........
d) 160 : 4 x 3 = ....................
Giá trị của biểu thức 160 : 4 x 3 là ............
a) 10 x 2 x 3 = 20 x 3 = 60
Giá trị của biểu thức 10 x 2 x 3 là 60.
b) 6 x 3 : 2 = 18 : 2 = 9
Giá trị của biểu thức 6 x 3 : 2 là 9.
c) 84 : 2 : 2 = 42 : 2 = 21
Giá trị của biểu thức 84 : 2 : 2 là 21.
d) 160 : 4 x 3 = 40 x 3 = 120
Giá trị của biểu thức 160 : 4 x 3 là 120.
10 x 2 x 3 = 60
6 x 3 : 2 = 9
HT tui chỉ kịp làm 2 câu đầu thui nha sorry tui fải đi ngủ đây
For i:= 1 to 30do x:=x+3 ; y:=y-x ; a) Vòng lặp với số lần biết trước trên chạy bao nhiêu vòng ? b) Giá trị đầu là gì ? c) Giá trị cuối là gì ? d) Câu lệnh của câu lệnh lặp với số lần biết trước là gì ? e) Tính giá trị của biến x và y , nếu biết trước giá trị của x và y?
\(B=\left(1-\frac{x^2}{x+2}\right)\cdot\frac{x^2+4x+4}{x}-\frac{x^2+6x+4}{x}\)
a, Tìm điều kiện của x để giá trị của biểu thức B được xác định
b,Rút gọn biểu thức B
c,Tính giá trị của B khi x=-3
d, Tìm giá trị của x để biểu thức B có giá trị lớn nhất. Tìm giá trị lớn nhất đó
a, ĐK: \(\hept{\begin{cases}x+2\ne0\\x\ne0\end{cases}\Rightarrow}\hept{\begin{cases}x\ne-2\\x\ne0\end{cases}}\)
b, \(B=\left(1-\frac{x^2}{x+2}\right).\frac{x^2+4x+4}{x}-\frac{x^2+6x+4}{x}\)
\(=\frac{-x^2+x+2}{x+2}.\frac{\left(x+2\right)^2}{x}-\frac{x^2+6x+4}{x}\)
\(=\frac{\left(-x^2+x+2\right)\left(x+2\right)-\left(x^2+6x+4\right)}{x}\)
\(=\frac{-x^3-2x^2+x^2+2x+2x+4-\left(x^2+6x+4\right)}{x}\)
\(=\frac{-x^3-2x^2-2x}{x}=-x^2-2x-2\)
c, x = -3 thỏa mãn ĐKXĐ của B nên với x = -3 thì
\(B=-\left(-3\right)^2-2.\left(-3\right)-2=-9+6-2=-5\)
d, \(B=-x^2-2x-2=-\left(x^2+2x+1\right)-1=-\left(x+1\right)^2-1\le-1\forall x\)
Dấu "=" xảy ra khi \(x+1=0\Rightarrow x=-1\)
Vậy GTLN của B là - 1 khi x = -1
1.Cho biểu thức C = x³/x²-4 - x/x-2 - 2/x+2
a,tìm giá trị của biến để biểu thức được xác định
b,Tìm x để C=0
c,Tìm giá trị nguyên của x để C nhận giá trị dương
2,cho P = (2+x/2-x + 4x²/x²-4 - 2-x/2+x): x²-3x/2x²-x³
a,Tìm điều kiện của x để giá trị của P được xác định
B, rút gọn P
c,Tính giá trị P với |x-5|=2
d,Tìm x để P<0
3,cho biểu thức B = [x+1/2x-2 + 3/x²-1 - x+3/2x+2]. 4x²-4/5
a,Tìm điều kiện của x để giá trị biểu thức được xác định
b,CMR khi giá trị của biểu thức không phụ thuộc vào giá trị của biến x?
4,Cho phân thức C = 3x²-x/9x²-6x+1
a, tìm điều kiện xác định phân thức
b,tính giá trị phân thức tại x=-8
c,Tìm x để giá trị của phân thức nhận giá trị dương
1.a)\(\frac{x^3}{x^2-4}-\frac{x}{x-2}-\frac{2}{x+2}\)
\(=\frac{x^3}{\left(x+2\right)\left(x-2\right)}-\frac{x}{x-2}-\frac{2}{x+2}\)
Để biểu thức được xác định thì:\(\left(x+2\right)\left(x-2\right)\ne0\)\(\Rightarrow x\ne\pm2\)
\(\left(x+2\right)\ne0\Rightarrow x\ne-2\)
\(\left(x-2\right)\ne0\Rightarrow x\ne2\)
Vậy để biểu thức xác định thì : \(x\ne\pm2\)
b) để C=0 thì ....
1, c , bn Nguyễn Hữu Triết chưa lm xong
ta có : \(/x-5/=2\)
\(\Rightarrow\orbr{\begin{cases}x-5=2\\x-5=-2\end{cases}}\Rightarrow\orbr{\begin{cases}x=7\\x=3\end{cases}}\)
thay x = 7 vào biểu thứcC
\(\Rightarrow C=\frac{4.7^2\left(2-7\right)}{\left(7-3\right)\left(2+7\right)}=\frac{-988}{36}=\frac{-247}{9}\)KL :>...
thay x = 3 vào C
\(\Rightarrow C=\frac{4.3^2\left(2-3\right)}{\left(3-3\right)\left(3+7\right)}\)
=> ko tìm đc giá trị C tại x = 3
chết mk nhìn nhầm phần c bài 2 :
\(2,\left(\frac{2+x}{2-x}+\frac{4x^2}{x^2-4}-\frac{2-x}{2+x}\right):\frac{x^2-3x}{2x^2-x^3}\)
Để P xác định
\(\Rightarrow2-x\ne0\Rightarrow x\ne2\)
\(2+x\ne0\Rightarrow x\ne-2\)
\(x^2-4\ne0\Rightarrow x\ne0\)
\(x^2-3x\ne0\Rightarrow x\ne3\)
b, \(P=\left(\frac{2+x}{2-x}+\frac{4x^2}{\left(2+x\right)\left(2-x\right)}+\frac{2-x}{2+x}\right):\frac{x\left(x-3\right)}{x^2\left(2-x\right)}\)
\(P=\left[\frac{4+4x+x^2}{\left(2-x\right)\left(2+x\right)}-\frac{4x^2}{\left(2+x\right)\left(2-x\right)}-\frac{4-4x+x^2}{\left(2+x\right)\left(2-x\right)}\right].\frac{x\left(2-x\right)}{x-3}\)
\(P=\left[\frac{8x-4x^2}{\left(2-x\right)\left(2+x\right)}\right].\frac{x\left(2-x\right)}{x-3}=\frac{4x\left(2-x\right)}{\left(2-x\right)\left(2+x\right)}.\frac{x\left(2-x\right)}{x-3}\)
\(P=\frac{4x^2\left(2-x\right)}{\left(x-3\right)\left(2+x\right)}\)
d, ĐỂ \(p=\frac{8x^2-4x^3}{x^2-x-6}< 0\)
\(TH1:8x^2-4x^3< 0\)
\(\Rightarrow8x^2< 4x^3\)
\(\Rightarrow2< x\Rightarrow x>2\)
\(TH2:x^2-x-6< 0\Rightarrow x^2< x+6\)
CHo phân thức \(\frac{x^2+2x+1}{x^2-1}\)
a, Với giá trị nào của x thì phân thức được xác định?
b, Rút gọn A
c, Tính giá trị của A tại x=-2
d, Tìm các gía trị nguyên của x để A có giá trị nguyên
a) Với giá trị của x thì phân thức được xác định là : \(x^2-1\ne0\)
=> \(x^2\ne\pm1\)
b) Rút gọn A : \(A=\frac{x^2+2x+1}{x^2-1}=\frac{\left(x+1\right)^2}{\left(x-1\right)\left(x+1\right)}=\frac{x+1}{x-1}\)
c) Tại x = -2 thì \(A=\frac{\left(-2\right)+1}{\left(-2\right)-1}=\frac{-1}{-3}=\frac{1}{3}\)
d) Ta có : \(A=\frac{x^2+2x+1}{x^2-1}=\frac{x+1}{x-1}=\frac{x-1+2}{x-1}=1+\frac{2}{x-1}\)
=> \(2⋮x-1\)=> x - 1 \(\in\)Ư(2) = { \(\pm1;\pm2\)}
+) x - 1 = 1 => x = 2 ; x - 1 = -1 => x = 0
+) x - 1 = 2 => x = 3 ; x - 1 = -2 => x = -1
Vậy : ....
a) Phân thức xác định
\(\Leftrightarrow x^2-1\ne0\)
\(\Leftrightarrow x\ne\pm1\)
Vậy với \(x\ne\pm1\)thì giá trị của phân thức đã cho xác định.
b) \(A=\frac{x^2+2x+1}{x^2-1}\)
\(\Leftrightarrow A=\frac{\left(x+1\right)^2}{\left(x-1\right)\left(x+1\right)}\)
\(\Leftrightarrow A=\frac{x+1}{x-1}\)
c) x = -2 ( thỏa mãn đkxđ )
Vậy \(A=\frac{-2+1}{-2-1}=\frac{-1}{-3}=\frac{1}{3}\)
d) A có giá trị nguyên
\(\Leftrightarrow\frac{x+1}{x-1}\)có giá trị nguyên
\(\Leftrightarrow\frac{x+1}{x-1}=\frac{x-1+2}{x-1}=1+\frac{2}{x-1}\)có giá trị nguyên
\(\Leftrightarrow x-1\inƯ\left(2\right)\)
\(\Leftrightarrow x=\left\{2;3;0\right\}\)
\(A=\frac{x^2+2x+1}{x^2-1}\)
a) ĐKXĐ : \(x^2-1\ne0\Rightarrow x\ne\pm1\)
b) \(A=\frac{x^2+2x+1}{x^2-1}=\frac{\left(x+1\right)^2}{\left(x+1\right)\left(x-1\right)}=\frac{x+1}{x-1}\)
c) Thế x = -2 ( tmđk ) vào A ta được :
\(A=\frac{-2+1}{-2-1}=\frac{-1}{-3}=\frac{1}{3}\)
Vậy A = 1/3 khi x = -2
d) \(A=\frac{x+1}{x-1}=\frac{x-1+2}{x-1}=1+\frac{2}{x-1}\)
Để A nguyên => \(\frac{2}{x-1}\)nguyên
=> \(2⋮x-1\)
=> \(x-1\inƯ\left(2\right)=\left\{\pm1;\pm2\right\}\)
=> \(x\in\left\{2;0;3;-1\right\}\)
Tìm điều kiện để phân thức \(\frac{2x-2}{x^2-x}\) được xác định
a) Tính giá trị của phân thức tại x=3 và x=0
b) Tính giá trị của x để phân thức có giá trị bằng 2
c) Tìm giá trị của x để phân thức có giá trị là số nguyên
Đặt phân thức đã cho là A
\(ĐKXĐ:x^2-x\ne0\)\(\Leftrightarrow x\left(x-1\right)\ne0\)\(\Leftrightarrow\hept{\begin{cases}x\ne0\\x-1\ne0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\ne0\\x\ne1\end{cases}}\)
a) \(A=\frac{2x-2}{x^2-x}=\frac{2\left(x-1\right)}{x\left(x-1\right)}=\frac{2}{x}\)
Với \(x=3\)( thoả mãn ĐKXĐ ) \(\Rightarrow A=\frac{2}{3}\)
Với \(x=0\)( không khoả mãn ĐKXĐ ) \(\Rightarrow\)Không tìm được giá trị của A
b) \(A=2\)\(\Leftrightarrow\frac{2}{x}=2\)\(\Leftrightarrow x=1\)( không thoả mãn ĐKXĐ )
Vậy không tìm được giá trị của x để \(A=2\)
c) A có giá trị nguyên \(\Leftrightarrow\frac{2}{x}\inℤ\)\(\Leftrightarrow2⋮x\)\(\Leftrightarrow x\inƯ\left(2\right)=\left\{\pm1;\pm2\right\}\)
So sánh với ĐKXĐ \(\Rightarrow x=1\)không thoả mãn
Vậy A nguyên \(\Leftrightarrow x\in\left\{-2;-1;2\right\}\)
ĐKXĐ:
----------->x khác 0
---------->(x-1) khác 0 ----------> x khác 1
VẠY ĐKXĐ LÀ X khác 0 và 1.
Bạn tự rút gọn nha
a, 2x-2\ x^2-x= 2\x
Thay x=3 vào biểu thức có:
-----> = 2\3
Vậy nếu thay x=3 vào biểu thức thì = 2\3
thay x=0 vào biểu thức có
------> = 0 vì 2\0=0
VẬY nếu thay x=0 thì biểu thức thì =0
b,
theo đề bài ta có
2\x=2
-----> 2:x=2
Vậy x=1
Câu c mik ko chắc nên bn tự làm nha
mik rất sorry:(((((((
\(x^2-x=x\left(x-1\right)\)
Phân thức xác định khi: \(\Leftrightarrow x\left(x-1\right)\ne0\Leftrightarrow\hept{\begin{cases}x\ne0\\x-1\ne0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\ne0\\x\ne1\end{cases}}\)
ĐKXĐ: \(x\ne0,x\ne1\)
a) Ta có: \(A=\frac{2x-2}{x^2-x}=\frac{2\left(x-1\right)}{x\left(x-1\right)}=\frac{2}{x}\)
+) Với x = 3
\(A=\frac{2}{3}\)
+) Với x = 0 (không tmđk)
=> Loại
\(A=2\Rightarrow\frac{2}{x}=2\Rightarrow x=1\)(không tmđk)
Cho phân thức 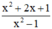
a) Với giá trị nào của x thì giá trị của phân thức được xác định ?
b) Chứng tỏ phân thức rút gọn của phân thức đã cho là 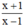
c) Để tính giá trị của phân thức đã cho tại x = 2 và x = -1, bạn Thắng đã làm như sau:
- Với x = 2, phân thức đã cho có giá trị là 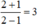
- Với x = -1, phân thức đã cho có giá trị là 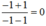
Em có đồng ý không ? Nếu không, em hãy chỉ ra chỗ mà em cho là sai.
Theo em, với những giá trị nào của biến thì có thể tính được giá trị của phân thức đã cho bằng cách tính giá trị của phân thức rút gọn ?
a) Phân thức 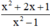 xác định
xác định
⇔ x2 – 1 ≠ 0
⇔ (x – 1)(x + 1) ≠ 0
⇔ x – 1 ≠ 0 và x + 1 ≠ 0
⇔ x ≠ ±1
Vậy phân thức xác định với mọi x ≠ ±1
b) Với x ≠ ±1, ta có:
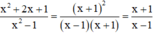
c) + Với x = 2, bạn Thắng tính giá trị biểu thức đúng.
+ Với x = -1, phân thức 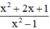 không xác định nên không thể tính giá trị biểu thức nên bạn Thắng tính sai.
không xác định nên không thể tính giá trị biểu thức nên bạn Thắng tính sai.
+ Để tính giá trị của phân thức bằng cách tính giá trị của phân thức rút gọn, ta phải đảm bảo giá trị của biến thỏa mãn điều kiện xác định.
1/ Tìm giá trị nhỏ nhất của biểu thức B= 2I3x-6I - 4
2/ Tìm x thuộc Z để biểu thức D= I x-2 I + I x-8 I đạt Gía trị nhỏ nhất
3/ Tìm GTNN của biểu thức B = I x-2017 I + I x-1 I
A= I x-2017 I + I x-2 I
4/ với giá trị nào của x,y thì biểu thức C = I x-100 I + I y+20 I - 1 có giá trị nhỏ nhất . Tìm GTNN
5/ Với giá trị nào của x thì biểu thức A= 100 - I x+5 I có giá trị lớn nhất. Tính GTLN đó
giúp với ạ ._.
1/ Gọi Bmin là GTNN của B
Ta có \(\left|3x-6\right|\ge0\)=> \(2\left|3x-6\right|\ge0\)với mọi \(x\in R\)
=> \(2\left|3x-6\right|-4\ge0\)với mọi \(x\in R\).
=> Bmin = 0.
Vậy GTNN của B = 0.
2/ Gọi Dmin là GTNN của D.
Ta có \(\left|x-2\right|\ge0\)với mọi \(x\in R\)
và \(\left|x-8\right|\ge0\)với mọi \(x\in R\)
=> \(\left|x-2\right|+\left|x-8\right|\ge0\)với mọi \(x\in R\)
=> Dmin = 0.
=> \(\left|x-2\right|+\left|x-8\right|=0\)
=> \(\hept{\begin{cases}\left|x-2\right|=0\\\left|x-8\right|=0\end{cases}}\)=> \(\hept{\begin{cases}x-2=0\\x-8=0\end{cases}}\)=> \(\hept{\begin{cases}x=2\\x=8\end{cases}}\)(Vô lý! Không thể cùng lúc có 2 giá trị x xảy ra)
Vậy không có x thoả mãn đk khi GTNN của D = 3.
Cho phân thức A = x^2 + 2x + 1 / x^2 - 1
a) Với giá trị nào của x thì giá trị của phân thức được xác định?
b) Rút gọn A.
c) Tính giá trị của A tại x = -2 .
a: ĐKXĐ: \(x\in\left\{1;-1\right\}\)
b: \(A=\dfrac{\left(x+1\right)^2}{\left(x-1\right)\left(x+1\right)}=\dfrac{x+1}{x-1}\)
\(a,ĐK:x\ne\pm1\\ b,A=\dfrac{\left(x+1\right)^2}{\left(x-1\right)\left(x+1\right)}=\dfrac{x+1}{x-1}\\ c,x=-2\Leftrightarrow A=\dfrac{-2+1}{-2-1}=\dfrac{-1}{-3}=\dfrac{1}{3}\)