Một mặt cầu (S) ngoại tiếp tứ diện đều cạnh a. Diện tích mặt cầu (S) là:
Đọc tiếp
Một mặt cầu (S) ngoại tiếp tứ diện đều cạnh a. Diện tích mặt cầu (S) là:
Những câu hỏi liên quan
Một mặt cầu có tâm nằm trong tứ diện đều cạnh a và mặt cầu đó tiếp xúc với 6 cạnh của tứ diện đó. Tính diện tích S của mặt cầu.
Đọc tiếp
Một mặt cầu có tâm nằm trong tứ diện đều cạnh a và mặt cầu đó tiếp xúc với 6 cạnh của tứ diện đó. Tính diện tích S của mặt cầu.
Một hình chóp tứ giác đều có cạnh đáy bằng cạnh bên và bằng a. Tính diện tích S của mặt cầu ngoại tiếp hình chóp A.
S
3
πa
2
2
B.
S
πa
2
2
C. S
2
πa
2
D.
S
πa
2
Đọc tiếp
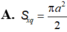
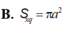
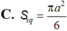
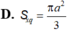
Một hình chóp tứ giác đều có cạnh đáy bằng cạnh bên và bằng a. Tính diện tích S của mặt cầu ngoại tiếp hình chóp
A. S = 3 πa 2 2
B. S = πa 2 2
C. S = 2 πa 2
D. S = πa 2
Gọi O là tâm hình vuông của mặt đáy. Khi đó O cũng là tâm của mặt cầu. Ta có:
R 2 = S O 2 = a 2 - a 2 2 2 = a 2 2 S = 4 πR 2 = 2 πa 2
Đáp án C
Đúng 0
Bình luận (0)
Một hình chóp tứ giác đều có cạnh đáy bằng cạnh bên và bằng a. Tính diện tích S của mặt cầu ngoại tiếp hình chóp
Đọc tiếp
Một hình chóp tứ giác đều có cạnh đáy bằng cạnh bên và bằng a. Tính diện tích S của mặt cầu ngoại tiếp hình chóp
Một hình chóp tứ giác đều có cạnh đáy bằng cạnh bên và bằng a. Tính diện tích S của mặt cầu ngoại tiếp hình chóp.
Đọc tiếp
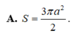
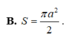
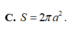
Một hình chóp tứ giác đều có cạnh đáy bằng cạnh bên và bằng a. Tính diện tích S của mặt cầu ngoại tiếp hình chóp.
Tính diện tích S của mặt cầu ngoại tiếp tứ diện AB’C’D’ biết ABCDA’B’C’D’ là hình lập phương cạnh a
Đọc tiếp
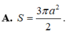
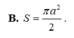
Tính diện tích S của mặt cầu ngoại tiếp tứ diện AB’C’D’ biết ABCDA’B’C’D’ là hình lập phương cạnh a
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a, các mặt bên tạo với đáy một góc
60
∘
. Tính diện tích S của mặt cầu ngoại tiếp hình chóp. A.
S
25
π
a
2
3
B.
S
32
π
a
2...
Đọc tiếp
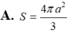
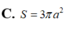
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a, các mặt bên tạo với đáy một góc 60 ∘ . Tính diện tích S của mặt cầu ngoại tiếp hình chóp.
A. S = 25 π a 2 3
B. S = 32 π a 2 3
C. S = 8 π a 2 3
D. S = a 2 12
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a, các mặt bên tạo với đáy một góc 60 độ. Tính diện tích S của mặt cầu ngoại tiếp hình chóp. A.
S
a
2
12
B.
S
25
π
a
2
3...
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a, các mặt bên tạo với đáy một góc 60 độ. Tính diện tích S của mặt cầu ngoại tiếp hình chóp.
A. S = a 2 12
B. S = 25 π a 2 3
C. . S = 32 π a 2 3
D. S = 8 π a 2 3
Cho tứ diện đều ABCD có độ dài cạnh bằng a, (S) là mặt cầu tiếp xúc với sáu cạnh của tứ diện ABCD, M là điểm thay đổi trên mặt cầu (S). Tính tổng
T
M
A
2
+
M
B
2
+
M
C
2
+
M
D
2
A.
3...
Đọc tiếp
Cho tứ diện đều ABCD có độ dài cạnh bằng a, (S) là mặt cầu tiếp xúc với sáu cạnh của tứ diện ABCD, M là điểm thay đổi trên mặt cầu (S). Tính tổng
T = M A 2 + M B 2 + M C 2 + M D 2
A. 3 a 2 8
B. a 2
C. 4 a 2
D. 2 a 2
Cho tứ diện đều ABCD có độ dài cạnh bằng a, (S) là mặt cầu tiếp xúc với sáu cạnh của tứ diện ABCD, M là điểm thay đổi trên mặt cầu (S). Tính tổng
T
M
A
2
+
M
B
2
+
M
C
2
+
M
D
2
. A.
3
a
2...
Đọc tiếp
Cho tứ diện đều ABCD có độ dài cạnh bằng a, (S) là mặt cầu tiếp xúc với sáu cạnh của tứ diện ABCD, M là điểm thay đổi trên mặt cầu (S). Tính tổng T = M A 2 + M B 2 + M C 2 + M D 2 .
A. 3 a 2 8
B. a 2
C. 4 a 2
D. 2 a 2
Đáp án D
Với tứ diện đều ABCD thì mặt cầu (S) là mặt cầu có tâm trùng với tâm của mặt cầu ngoại tiếp tứ diện ABCD và là trọng tâm của tứ diện đều cạnh a, đồng thời có bán kính R = a 2 4
Gọi G là trọng tâm của tứ diện ⇒ G A ¯ + G B ¯ + G C ¯ + G D ¯ = 0 ¯
Ta có:
T = M A 2 + M B 2 + M C 2 + M D 2 = M G ¯ + G A ¯ 2 + M G ¯ + G B ¯ 2 + M G ¯ + G C ¯ 2 + M G ¯ + G D ¯ 2
= 4 M G 2 + 2 M G ¯ G A ¯ + G B ¯ + G C ¯ + G D ¯ ⏟ 0 + G A 2 + G B 2 + G C 2 + G D 2 = 4 M G 2 + 4 G A 2
= 4 a 2 4 2 + 4 a 6 4 2 = 2 a 2 . Vậy T = M A 2 + M B 2 + M C 2 + M D 2 = 2 a 2
Đúng 0
Bình luận (0)