cho hình thang ABCD có AB=60cm,CD=90cm,AH=30cm.Trên AD lấy E sao cho DE=1 phần 3 AD.Từ E kẻ đường thẳng song song với AB và CD cắt BC tại F.
a.Tính diện tich tam giác EFCD
b.so sánh EF và CD
Cho hình thang ABCD có AB song song với CD. Biết AB = 60cm, CD = 90cm, đường cao AH = 30cm. Trên cạnh AD lấy điểm E sao cho DE = 1/3 AD. Kẻ EF song song với DC. F nằm trên cạnh BC. Hãy so sánh EF và DC.
a) Nối A với F 
Và D với F
Ta có:
ED=1/3 AD
S(EFD) = 1/3 S(AFD)
Vì đáy ED= 1/3 AD ; d.c hạ từ F chung
Nếu lấy EF làm đáy => đ.c hạ từ D= 1/3 đ.c hạ từ A
=>đ.c của tam giác EFD là 30 x 1/3 = 10 = đ.c của tam giác FCD
=>đ.c của tam giác AEF là 30 x (1 – 1/3 ) = 20 = đ.c của tam giác ABF
S(ABF) = 60 x 20 : 2 = 600 cm2
S ( FCD)= 90 x 10 : 2 =450 cm2
S ( ABCD)= (90+60) x 30 : 2 = 2250 cm2
Mà S( AFD ) = S(ABCD) – S (ABF) – S (FCD)
S (AFD )= 2250 – 600 – 450 = 1200 cm2
S(EFD ) = 1200 : 3 = 400
=> S(EDFC) = 400 + 450 = 850 (cm2)
b) S(EFD ) / S( FCD) = 400/450 = 8/9
vậy EF = 8/9 CD
a) Nối A với F
Và D với F
Ta có:
ED=1/3 AD
=> ED= ½ AD
S(EFD) = 1/3 S(AFD)
Vì đáy ED= 1/3 AD ; d.c hạ từ F chung
Nếu lấy EF làm đáy => đ.c hạ từ D= 1/3 đ.c hạ từ A
=>đ.c của tam giác EFD là 30 x 1/3 = 10 = đ.c của tam giác FCD
=>đ.c của tam giác AEF là 30 x (1 – 1/3 ) = 20 = đ.c của tam giác ABF
S(ABF) = 60 x 20 : 2 = 600 cm2
S ( FCD)= 90 x 10 : 2 =450 cm2
S ( ABCD)= (90+60) x 30 : 2 = 2250 cm2
Mà S( AFD ) = S(ABCD) – S (ABF) – S (FCD)
S (AFD )= 2250 – 600 – 450 = 1200 cm2
S(EFD ) = 1200 : 3 = 400
=> S(EDFC) = 400 + 450 = 850 (cm2)
b) S(EFD ) / S( FCD) = 400/450 = 8/9
vậy EF = 8/9 CD
cho hình thang ABCD có độ dài đáy AB=60cm , CD=90cm . chiều cao AH = 30cm . trên AD lấy điểm E sao cho DE=1/3AD . từ E kẻ song song với 2 đáy cắt BC tại F
a, tính diện tích hình EFCD
b, so sánh EF và CD
mị ko bít đâu à nha
vả lại tui cũng ddang gặp câu này mà bó tay.Các ae học giỏi giúp mị với
a) Nối A với F 
Và D với F
Ta có:
ED=1/3 AD
=> ED= ½ AD
S(EFD) = 1/3 S(AFD)
Vì đáy ED= 1/3 AD ; d.c hạ từ F chung
Nếu lấy EF làm đáy => đ.c hạ từ D= 1/3 đ.c hạ từ A
=>đ.c của tam giác EFD là 30 x 1/3 = 10 = đ.c của tam giác FCD
=>đ.c của tam giác AEF là 30 x (1 – 1/3 ) = 20 = đ.c của tam giác ABF
S(ABF) = 60 x 20 : 2 = 600 cm2
S ( FCD)= 90 x 10 : 2 =450 cm2
S ( ABCD)= (90+60) x 30 : 2 = 2250 cm2
Mà S( AFD ) = S(ABCD) – S (ABF) – S (FCD)
S (AFD )= 2250 – 600 – 450 = 1200 cm2
S(EFD ) = 1200 : 3 = 400
=> S(EDFC) = 400 + 450 = 850 (cm2)
b) S(EFD ) / S( FCD) = 400/450 = 8/9
vậy EF = 8/9 CD
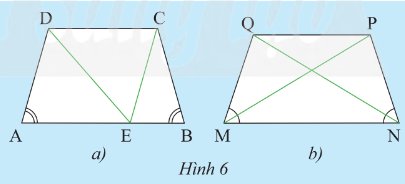
a) Cho hình thang cân \(ABCD\) có hai đáy là \(AB\) và \(CD\) (\(AB > CD\). Qua \(C\) vẽ đường thẳng song song với \(AD\) và cắt \(AB\) tại \(E\) (Hình 6a)
i) Tam giác \(CEB\) là tam giác gì? Vì sao?
ii) So sánh \(AD\) và \(BC\)
b) Cho hình thang cân \(MNPQ\) có hai đáy là \(MN\) và \(PQ\) (Hình 6). So sánh \(MP\) và \(NQ\)
a) i) \(ABCD\) là hình thang cân (gt)
\( \Rightarrow \widehat A = \widehat B\) (1) và \(DC\) // \(AE\)
Vì \(AD\;{\rm{//}}\;CE\) (gt)
\(\widehat A = \widehat {CEB}\) (cặp góc đồng vị) (2)
Từ (1) và (2) suy ra: \(\widehat {CEB} = \widehat B\)
Suy ra \(\Delta CEB\) là tam giác cân.
ii) \(\Delta CEB\) cân tại \(C\) (cmt)
Suy ra: \(CE = BC\) (3)
Xét \(\Delta ADE\) và \(\Delta CED\) ta có:
\(\widehat {{\rm{ADE}}} = \widehat {{\rm{CED}}}\) (\(AD\)// \(CE\), cặp góc so le trong)
\(DE\) chung
\(\widehat {{\rm{AED}}} = \widehat {{\rm{CDE}}}\) (\(CD\) // \(AB\), cặp góc so le trong)
Suy ra: \(\Delta ADE = \Delta CED\) (g-c-g)
Suy ra: \(AD = CE\) (4)
Từ (3) và (4) suy ra: \(AD = BC\)
b) Chứng minh tương tự như ý a) ta có: Hình thang cân \(MNPQ\) có hai cạnh bên \(MQ = NP\)
Xét tam giác \(\Delta MQP\) và \(\Delta NPQ\) ta có:
\(MQ = NP\) (cmt)
\(\widehat {{\rm{MQP}}} = \widehat {{\rm{NPQ}}}\) (do \(MNPQ\) là hình thang cân)
\(PQ\) chung
Suy ra: \(\Delta MQP = \Delta NPQ\) (c-g-c)
\( \Rightarrow MP = NQ\) (hai cạnh tương ứng)
Bài 1: Cho hình thang ABCD ( có AB// CD). Gọi E là trung điểm của AD. Kẻ đường thẳng qua E song song với AB và cắt BC tại F.
a) Chứng minh F là trung điểm của BC.
b) Cho AB = 4; CD =12. Tính EF.
Bài 2: Cho hình thang ABCD (có AB // CD; AB < CD). Gọi E, F, G lần lượt là trung điểm của AD, AC, BD.
a) Chứng minh E, F, G thẳng hàng.
b) Chứng minh EF = (CD-AB)/2.
Bài 1: Cho hình thang ABCD ( có AB// CD). Gọi E là trung điểm của AD. Kẻ đường thẳng qua E song song với AB và cắt BC tại F.
a) Chứng minh F là trung điểm của BC.
b) Cho AB = 4; CD =12. Tính EF.
Bài 2: Cho hình thang ABCD (có AB // CD; AB < CD). Gọi E, F, G lần lượt là trung điểm của AD, AC, BD.
a) Chứng minh E, F, G thẳng hàng.
b) Chứng minh EF = (CD-AB)/2.
Cho hình thang ABCD (AB // CD) có CD>AB. Qua A kẻ đường thẳng song song với BC cắt CD, BD tại K,E. qua B kẻ đường thẳng song song với AD cắt CD, AC tại I, F .chứng minh AB // EF
cho hình thang cân ABCD có đáy CD và AB ( AB<CD).Qua A kẻ đường thẳng song song với BC cắt đường chéo BD ở E qua B kẻ đường thẳng song song với AD cắt đường thẳng song song với AD cắt đường chéo AC tại F . a) CMR tứ giác DEFC là hình thang cân . b) tính độ dài EF biết AB=5cm , CD= 10cm
HELP ME ...............
Cho hình thang ABCD ( AB // CD). E là trung điểm AD. Từ E kẻ đường thẳng song song với AB và cắt BC tại F. Biết AB=15cm, EF=35cm. Tìm CD
Xét hình thang ABCD có :
E là trung điểm của AD
EF//AB//CD (Vì EF vàCD cùng // với AB )
=) EF là đường trung bình cua hình thang ABCD
=) EF= (AB+CD):2
Thay số vào biểu thức trên ta được :
35=(15+CD) :2
15+CD=35.2
15+CD=70
CD= 70-15
CD= 55 (cm)
Vậy CD=55 cm
Cho hình thang ABCD có AB//Cd. Trên AD lấy 2 điểm M và E sao cho AM=ME=ED. QUa M và E kẻ các đường thằng song song với AB cắt BC lần lượt tại N và F. Biết AB=12cm,EF=18cm. ĐỘ dài CD là
Hình thang ABCD (AB//CD) có: M là trung điểm AE, MN//AB//EF.
\(\Rightarrow\)N là trung điểm BF nên MN là đường trung bình của hình thang ABCD.
\(\Rightarrow MN=\dfrac{AB+EF}{2}=\dfrac{12+18}{2}=15\left(cm\right)\).
Hình thang MNCD (MN//CD) có: E là trung điểm MD, EF//MN//CD.
\(\Rightarrow\)F là trung điểm CD nên EF là đường trung bình của hình thang MNCD.
\(\Rightarrow EF=\dfrac{MN+CD}{2}\Rightarrow CD=2EF-MN=2.18-15=21\left(cm\right)\)