Có bao nhiêu giá trị nguyên của m để phương trình cos 2 x − 4 cos x − m = 0 có nghiệm.
A. 6
B. 7
C. 8
D. 9
Có bao nhiêu giá trị nguyên của m để phương trình cos 2x – 4. cos x – m = 0 có nghiệm.
A. 6
B. 7
C. 8
D. 9
Có bao nhiêu giá trị nguyên của tham số m để phương trình sin 2 x + cos 2 x + | sin x + cos x | - cos 2 x + m - m = 0 có nghiệm thực?
A. 9
B. 2
C. 3
D. 5
Đáp án C
Sử dụng tính đơn điệu của hàm số, đánh giá số nghiệm của phương trình.
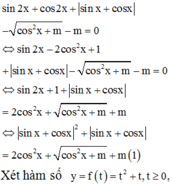
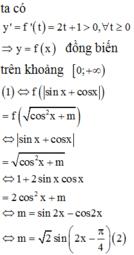

Vậy, có 3 giá trị nguyên của m thỏa mãn yêu cầu đề bài.
Có bao nhiêu giá trị nguyên của tham số m để phương trình
m + 3 . m + cos x 3 3 = cos x có nghiệm thực?
A. 2.
B. 7.
C. 5.
D. 3.
Cho phương trình m. sin x + 4. cos x = 2m - 5 với m là tham số. Có bao nhiêu giá trị nguyên của m để phương trình có nghiệm?
A. 4
B. 7.
C. 6.
D. 5
Có bao nhiêu giá trị nguyên của tham số m để phương trình cos 3 x - cos 2 x + m cos x = 1 có đúng 7 nghiệm khác nhau thuộc khoảng - π 2 ; 2 π
A. 2
B. 4
C. Không tồn tại
D. 1
Chọn D.
Phương pháp: Biện luận nghiệm của phương trình theo m.
Cách giải: Ta có:
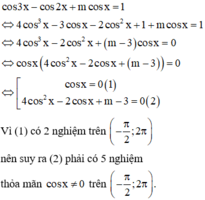

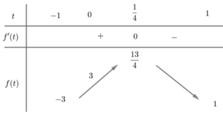

Có bao nhiêu giá trị nguyên của tham số m để phương trình 1 + 2 cos x + 1 + 2 sin x = 1 2 m có nghiệm?
A. 3.
B. 5.
C. 4.
D. 2.
Tổng tất cả các giá trị nguyên của m để phương trình 4 sin x + ( m - 4 ) cos x - 2 m + 5 = 0 có nghiệm là:
A. 5
B. 6
C. 10
D. 3
Số giá trị nguyên m để phương trình 4 m - 4 . sin x . cos x + m - 2 . cos 2 x = 3 m - 9 . Có nghiệm là:
A. 7
B. 6
C. 5
D. 4
Số các giá trị nguyên của m để phương trình ( cos x + 1).(4.cos 2x – m.cos x) = m.sin2x có đúng 2 nghiệm x ∈ 0 , 2 π 3 là:
A. 3.
B. 0.
C. 2.
D. 1.