Một khối lăng trụ tam giác có thể phân chia ít nhất thành n tứ diện có thể tích bằng nhau. Khẳng định nào sau đây là đúng?
A. n = 3
B. n = 6
C. n = 4
D. n = 8.
Những câu hỏi liên quan
Cho lăng trụ tam giác ABC.MNP có thể tích V. Gọi
G
1
;
G
2
;
G
3
;
G
4
lần lượt là trọng tâm của các tam giác ABC, ACM, AMB, BCM,
V
1
là thể tích của khối tứ diện
G
1
G
2
G
3
G
4
.
Khẳng định nào sau đây là đú...
Đọc tiếp
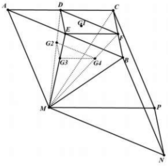
Cho lăng trụ tam giác ABC.MNP có thể tích V. Gọi G 1 ; G 2 ; G 3 ; G 4 lần lượt là trọng tâm của các tam giác ABC, ACM, AMB, BCM, V 1 là thể tích của khối tứ diện G 1 G 2 G 3 G 4 . Khẳng định nào sau đây là đúng?
A. V = 27 V 1
B. V = 9 V 1
C. V = 81 V 1
D. 8 V = 81 V 1
Đáp án C.
Phương pháp
So sánh diện tích đáy và chiều cao của các khối chóp.
Cách giải
Gọi D, E, F lần lượt là trung điểm của AC, AB, BC.
Vì G 2 ; G 3 ; G 4 là trọng tâm các tam giác MAC, MAB, MBC nên
G 2 ∈ M D ; M G 2 = 2 D G 2 G 3 ∈ M E ; M G 3 = 2 E G 3 G 4 ∈ M F ; M G 4 = 2 F G 4 ⇒ G 2 G 3 G 4 / / D E F ⇒ V 1 = V E . G 2 G 3 G 4 = F G 3 M G 3 . V M . G 2 G 3 G 4 = 1 2 V M . G 2 G 3 G 4
Lại có
V M . G 2 G 3 G 4 V M D E F = M G 2 . M G 3 . M G 4 M D . M E . M F = 2 3 . 2 3 . 2 3 = 8 27
⇒ V 1 = 1 2 8 27 V M D E F = 4 27 V M D E F
Lại có
S D E F = 1 4 S A B C ⇒ V M . D E F = 1 4 V M . A B C = 1 4 . 1 3 V = 1 12 V
Vậy
V 1 = 4 27 . V 12 = V 81
Đúng 0
Bình luận (0)
Cho khối đa diện như hình vẽ bên. Trong đó ABC.A B C là khối lăng trụ tam giác đều có tất cả các cạnh đều bằng 1, S.ABC khối chóp tam giác đều có cạnh bên SA2/3. Mặt phẳng (SA B ) chia khối đa diện đã cho thành hai phần. Gọi
V
1
là thể tích phần khối đa diện chứa đỉnh A,
V
2
là thể tích phần khối đa diện không chứa đỉnh A. Mệnh đề nào sau đây đúng A.
72
V
1...
Đọc tiếp
Cho khối đa diện như hình vẽ bên. Trong đó ABC.A' B' C' là khối lăng trụ tam giác đều có tất cả các cạnh đều bằng 1, S.ABC khối chóp tam giác đều có cạnh bên SA=2/3. Mặt phẳng (SA' B' ) chia khối đa diện đã cho thành hai phần. Gọi V 1 là thể tích phần khối đa diện chứa đỉnh A, V 2 là thể tích phần khối đa diện không chứa đỉnh A. Mệnh đề nào sau đây đúng
A. 72 V 1 = 5 V 2
B. 3 V 1 = V 2
C. 24 V 1 = 5 V 2
D. 4 V 1 = 5 V 2
Cho hình lăng trụ đứng
A
B
C
.
A
1
B
1
C
1
có đáy ABC là tam giác vuông tại B, AB 4, BC6; chiều cao của lăng trụ bằng 10. Gọi K, M, N lần lượt là trung điểm của các cạnh
B
B
1
,
A
1
B
1
,
B...
Đọc tiếp
Cho hình lăng trụ đứng A B C . A 1 B 1 C 1 có đáy ABC là tam giác vuông tại B, AB= 4, BC=6; chiều cao của lăng trụ bằng 10. Gọi K, M, N lần lượt là trung điểm của các cạnh B B 1 , A 1 B 1 , B C . Thể tích của khối tứ diện C 1 K M N là
A. 15.
B. 5.
C. 45.
D. 10.
Cho hình lăng trụ đứng
A
B
C
.
A
1
B
1
C
1
có đáy ABC là tam giác vuông tại B, AB 4, BC6; chiều cao của lăng trụ bằng 10. Gọi K, M, N lần lượt là trung điểm của các cạnh
B
B
1
,
A
1
B
1
,
B...
Đọc tiếp
Cho hình lăng trụ đứng A B C . A 1 B 1 C 1 có đáy ABC là tam giác vuông tại B, AB= 4, BC=6; chiều cao của lăng trụ bằng 10. Gọi K, M, N lần lượt là trung điểm của các cạnh B B 1 , A 1 B 1 , B C . Thể tích của khối tứ diện C 1 K M N là
A. 15
B. 5
C. 45
D. 10
Trong không gian với hệ tọa độ Oxyz, hình lăng trụ có diện tích đáy bằng 5 (đvdt) và hai đáy là hai tam giác nằm trên hai mặt phẳng
α
,
β
có phương trình lần lượt là
α
:
x
−
2
y
+
3
z
−
a
0
và
β
:
3
x
−
6
y
+
9
z...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, hình lăng trụ có diện tích đáy bằng 5 (đvdt) và hai đáy là hai tam giác nằm trên hai mặt phẳng α , β có phương trình lần lượt là α : x − 2 y + 3 z − a = 0 và β : 3 x − 6 y + 9 z + b = 0 ( a , b ∈ ℝ + , b ≠ 3 a ) . Hỏi nếu thể tích khối lăng trụ bằng 5 14 thì khẳng định nào sau đây là đúng?
A. 3 a + b = 14
B. a + b 3 = 42
C. 3 a + b = 14
D. a + b 3 = 14
Trong không gian với hệ tọa độ Oxyz, hình lăng trụ có diện tích đáy bằng 5 (đvdt) và hai đáy là hai tam giác nằm trên hai mặt phẳng
α
,
β
có phương trình lần lượt là
α
:
x
−
2
y
+
3
z
−
a
0
và
β
:
3
x
−
6
y...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, hình lăng trụ có diện tích đáy bằng 5 (đvdt) và hai đáy là hai tam giác nằm trên hai mặt phẳng α , β có phương trình lần lượt là α : x − 2 y + 3 z − a = 0 và β : 3 x − 6 y + 9 z + b = 0 ( a , b ∈ ℝ + , b ≠ 3 a ) . Hỏi nếu thể tích khối lăng trụ bằng 5 14 thì khẳng định nào sau đây là đúng?
A. 3 a + b = 14
B. a + b 3 = 42
C. 3 a + b = 14
D. a + b 3 = 14
Đáp án D
Ta có
α : x − 2 y + 3 z − a = 0 ⇔ 3 x − 6 y + 9 z − 3 a = 0.
Gọi h là chiều cao của hình lăng trụ, do α / / β nên h = d α ; β = b + 3 a 3 14 .
Ta có
V = S . h ⇔ 5 14 = 5. b + 3 a 3 14 = 3 a + b = 42 ⇔ a + b 3 = 14
Đúng 0
Bình luận (0)
Cho lăng trụ tam giác ABC.A′B′C′. Gọi M,N,P lần lượt là trung điểm các cạnh A′B′,BC,CC′. Mặt phẳng (MNP) chia khối lăng trụ thành hai phần, phần chưa điểm B có thể tích là
V
1
.
Gọi V là thể tích khối lăng trụ. Tính
V
1
V
. A.
25
288
B.
29
144
C.
37...
Đọc tiếp
Cho lăng trụ tam giác ABC.A′B′C′. Gọi M,N,P lần lượt là trung điểm các cạnh A′B′,BC,CC′. Mặt phẳng (MNP) chia khối lăng trụ thành hai phần, phần chưa điểm B có thể tích là V 1 . Gọi V là thể tích khối lăng trụ. Tính V 1 V .
A. 25 288
B. 29 144
C. 37 288
D. 19 144
Cho khối lăng trụ đứng ABC.A′B′C′ có đáy là tam giác vuông cân tại C, AB 2a. Trên các đoạn thẳng AB′, A′C có lần lượt các điểm M, N và P, Q sao cho MNPQ là tứ diện đều. Tính thể tích của khối lăng trụ ABC.A′B′C′.
Đọc tiếp
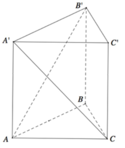
Cho khối lăng trụ đứng ABC.A′B′C′ có đáy là tam giác vuông cân tại C, AB = 2a. Trên các đoạn thẳng AB′, A′C có lần lượt các điểm M, N và P, Q sao cho MNPQ là tứ diện đều. Tính thể tích của khối lăng trụ ABC.A′B′C′.
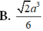
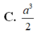
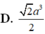
Chọn C
Gọi h là độ dài cạnh bên của lăng trụ đứng đã cho.
Vì MNPQ là tứ diện đều nên
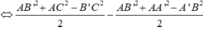= 0
*Chú ý một khối tứ diện đều (tất cả các cạnh bằng nhau) hoặc một khối tứ diện gần đều (độ dài cặp cạnh đối bằng nhau) thì cặp cạnh đối của chúng vuông góc với nhau (xem chương góc và khoảng cách).
*Chú ý tích vô hướng cho hai véctơ cùng gốc
Đúng 0
Bình luận (0)
Cho lăng trụ tam giác đều
A
B
C
.
A
B
C
. Trên
A
B
kéo dài lấy điểm M sao cho
B
M
1
2
A
B
. Gọi N, P lần lượt là trung điểm của
A
C
và
B
B
. Mặt phàng (MNP) chia khối lăng trụ
A...
Đọc tiếp
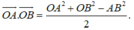
Cho lăng trụ tam giác đều A B C . A ' B ' C ' . Trên A ' B ' kéo dài lấy điểm M sao cho B ' M = 1 2 A ' B . Gọi N, P lần lượt là trung điểm của A ' C ' và B ' B ' . Mặt phàng (MNP) chia khối lăng trụ A B C . A ' B ' C ' thành hai khối đa diện, trong đó khối đa diện chứa đỉnh A ' có thể tích V 1 , khối đa diện chứa đỉnh C ' có thể tích V 2 . Tỉ số V 1 V 2 là:
A. V 1 V 2 = 49 95
B. V 1 V 2 = 49 144
C. V 1 V 2 = 95 144
D. V 1 V 2 = 97 59
