Trong không gian Oxyz, cho tứ diện ABCD với A m ; 0 ; 0 , B 0 ; m - 1 ; 0 , C 0 ; 0 ; m + 4 thỏa mãn B C = A D , C A = B D v à A B = C D . Giá trị nhỏ nhất của bán kính mặt cầu ngoại tiếp tứ diện ABCD bằng
A. 7 2
B. 14 2
C. 7
D. 14
Trong không gian với hệ trục tọa độ Oxyz, cho tứ diện ABCD với A 0 ; 1 ; 1 , B 0 ; 2 ; 1 , C − 1 ; 0 ; 2 , D − 3 ; 2 ; 5 . Tính thể tích tứ diện ABCD.
A. 1 6
B. 1
C. 1 3
D. 1 2
Trong không gian Oxyz, cho tứ diện ABCD với A(1;2;1), B(2;1;3), C(3;2;2), D(1;1;1). Độ dài chiều cao DH của tứ diện bằng
A. 3 14 14
B. 14 14
C. 4 14 7
D. 3 14 7
Trong không gian Oxyz, cho tứ diện ABCD với A(-1;-2;4), B(-4;-2;0), C(3;-2;1), D(1;1;1). Độ dài đường cao của tứ diện ABCD kẻ từ đỉnh D bằng
A. 3
B. 1
C. 2
D. 1 2
Trong không gian Oxyz, cho tứ diện ABCD với , B − 4 ; − 2 ; 0 , C 3 ; − 2 ; 1 , D 1 ; 1 ; 1 . Độ dài đường cao của tứ diện ABCD kẻ từ đỉnh D bằng
A. 3
B. 1
C. 2
D. 1 2
Trong không gian Oxyz, cho tứ diện ABCD với A(2;-4;6), B(1;1;1), C(0;3;0), D(0;0;3). Viết phương trình tham số của đường thẳng d chứa đường cao AH của tứ diện ABCD
A. x = 2 + t, y = -4 - t, z = 6 + t
B. x = 1 + 2t, y = -1 -4t, z = 1 + 6t
C. x = 2 + t, y = -4 + t, z = 6 + t
D. x = 1 + 2t, y = 1 - 4t, z = 1 + 6t
Trong không gian tọa độ Oxyz, cho tứ diện ABCD có A(1;0;0), B(0;1;0), C(0;0;1), D(-2;1;-1). Thể tích của tứ diện ABCD bằng
A. 1
B. 2
C. 1 2
D. 1 3
Chọn đáp án C.
Ta có
![]()
![]()
Áp dụng công thức ta có:
V A B C D = 1 6 A B ⇀ . A C ⇀ . A D ⇀ = 1 2
Trong không gian tọa độ Oxyz, cho tứ diện ABCD với A(-1;-2;4), B(-4;-2;0), C(3;-2;1) và D(1;1;1) . Độ cao của tứ diện kẻ từ D bằng
A. 3.
B. 1.
C. 2.
D. 0,5
Trong không gian Oxyz, cho tứ diện ABCD có A ( 1 ; 0 ; 2 ) , B ( - 2 ; 1 ; 3 ) , C ( 3 ; 2 ; 4 ) , D ( 6 ; 9 ; - 5 ) . Tìm tọa độ trọng tâm G của tứ diện ABCD
A. G - 9 ; 18 4 ; - 30
B. G(8;12;4)
C. G 3 ; 3 ; 14 4
D. G(2;3;1)
Chọn D.
Gọi G(a,b,c) là trọng tâm của tứ diện, ta có:
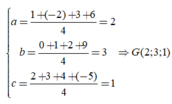
Trong không gian Oxyz, cho tứ diện ABCD có A ( 1 ; 0 ; 2 ) , B ( - 2 ; 1 ; 3 ) , C ( 3 ; 2 ; 4 ) , D ( 6 ; 9 ; - 5 ) . Tìm tọa độ trọng tâm G của tứ diện ABCD
A. G - 9 ; 18 4 ; - 30
B. G(8;12;4)
C. G 3 ; 3 ; 14 4
D. G(2;3;1)
Chọn D.
Gọi G(a,b,c) là trọng tâm của tứ diện, ta có: