Giải các phương trình sau trên tập hợp số phức:
z 4 + z 2 - 6 = 0
Những câu hỏi liên quan
Giải các phương trình sau trên tập hợp số phức:
a) z4 + z2 – 6 = 0; b) z4 + 7z2 + 10 = 0
a) \(z^4+z^2-6=0\)
\(\Leftrightarrow z^4+3z^2-2z^2-6=0\)
\(\Leftrightarrow z^2\left(z^2+3\right)-2\left(z^2+3\right)=0\)
\(\Leftrightarrow\left(z^2+3\right)\left(z^2-2\right)=0\)
\(\Leftrightarrow z^2-2=0\) ( Vì: \(\left(z^2+3>0\right)\) )
\(\Leftrightarrow\left[\begin{array}{nghiempt}z=\sqrt{2}\\z=-\sqrt{2}\end{array}\right.\)
b) \(z^4+7z^2+10=0\)
\(\Leftrightarrow z^4+2z^2+5z^2+10=0\)
\(\Leftrightarrow z^2\left(z^2+2\right)+5\left(z^2+2\right)=0\)
\(\Leftrightarrow\left(z^2+2\right)\left(z^2+5\right)=0\) (vô nghiệm)
Vậy hp vô nghiêm
Đúng 0
Bình luận (4)
Trần Việt Linh:số phức kìa chưa học đừng làm
Đúng 0
Bình luận (3)
b) ra \(\pm\sqrt{2}i\) và \(\pm\sqrt{5}i\) ms đúng vô nghiệm cái....
Đúng 0
Bình luận (0)
Giải các phương trình sau trên tập hợp số phức:
a) z4 + z2 – 6 = 0; b) z4 + 7z2 + 10 = 0
Giải các phương trình sau trên tập hơn số phức :
a) \(z^4+z^2-6=0\)
b) \(z^4+7z^2+10=0\)
a) Đặt Z = z2 , ta được phương trình Z2 + Z – 6 = 0
Phương trình này có hai nghiệm là Z1 = 2, Z2 = -3
Vậy phương trình có bốn nghiệm là ± √2 và ± i√3.
b) Đặt Z = z2 , ta được phương trình Z2 + 7Z + 10 = 0
Phương trình này có hai nghiệm là Z1 = -5, Z2 = -2
Vậy phương trình có bốn nghiệm là ± i√2 và ± i√5.
Đúng 0
Bình luận (0)
Trên tập số phức, cho phương trình sau : ( z + i)4 + 4z2 0. Có bao nhiêu nhận xét đúng trong số các nhận xét sau? 1. Phương trình vô nghiệm trên trường số thực R. 2. Phương trình vô nghiệm trên trường số phức C 3. Phương trình không có nghiệm thuộc tập số thực. 4. Phương trình có bốn nghiệm thuộc tập số phức. 5. Phương trình chỉ có hai nghiệm là số phức. 6. Phương trình có hai nghiệm là số thực A. 0. B. 1. C. 3. D. 2.
Đọc tiếp
Trên tập số phức, cho phương trình sau : ( z + i)4 + 4z2 = 0. Có bao nhiêu nhận xét đúng trong số các nhận xét sau?
1. Phương trình vô nghiệm trên trường số thực R.
2. Phương trình vô nghiệm trên trường số phức C
3. Phương trình không có nghiệm thuộc tập số thực.
4. Phương trình có bốn nghiệm thuộc tập số phức.
5. Phương trình chỉ có hai nghiệm là số phức.
6. Phương trình có hai nghiệm là số thực
A. 0.
B. 1.
C. 3.
D. 2.
Chọn D.
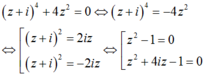
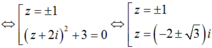
Do đó phương trình có 2 nghiệm thực và 4 nghiệm phức. Vậy nhận xét 4, 6 đúng.
Đúng 0
Bình luận (0)
Giải các phương trình sau trên tập hợp số phức :
a) \(-3z^2+2z-1=0\)
b) \(z^4+7z^2+10=0\)
a) Ta có ∆' = 1 - 3 = -2.
Vậy nghiệm của phương trình là z1,2 =
b) Ta có ∆ = 9 - 56 = -47.
Vậy nghiệm của phương trình là z1,2 = ;
c) Ta có ∆ = 49 - 4.5.11 = -171.
Vậy nghiệm của phương trình là z1,2 =
Đúng 0
Bình luận (0)
Giải các phương trình sau trên tập số phức:
(3 + 2i)z - (4 + 7i) = 2 - 5i
(3 + 2i).z - (4 + 7i) = 2 – 5i
⇔ (3 + 2i).z = (2 – 5i) + (4 + 7i)
⇔ (3 + 2i).z = 6 + 2i
Đúng 0
Bình luận (0)
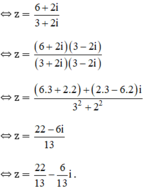
Giải các phương trình sau trên tập số phức:
(7 - 3i)z + (2 + 3i) = (5 - 4i)z
(7 - 3i)z + (2 + 3i) = (5 - 4i).z
⇔ [(7 – 3i) – (5 – 4i)].z = - (2 + 3i)
⇔ (2 + i).z = -(2 + 3i)
Đúng 0
Bình luận (0)
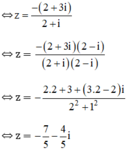
Giải các phương trình sau trên tập số phức :
a) \(3z^2+7z+8=0\)
b) \(z^4-8=0\)
c) \(z^4-1=0\)
a) 3z2 + 7z + 8 = 0 có Δ = 49 – 4.3.8 = -47
Vậy phương trình có hai nghiệm là: z1,2=−7±i√476z1,2=−7±i476
b) z4 – 8 = 0
Đặt Z = z2, ta được phương trình : Z2 – 8 = 0
Suy ra: Z = ± √8
Vậy phương trình đã cho có 4 nghiệm là: z1,2=±4√8,z3,4=±i4√8z1,2=±84,z3,4=±i84
c) z4 – 1 = 0 ⇔ (z2 – 1)(z2 + 1) = 0
Vậy phương trình đã cho có 4 nghiệm là ±1 và ±i
Đúng 0
Bình luận (0)
Giải phương trình: ( z - i ) 2 + 4 = 0 trên tập số phức.
(Đề thi tốt nghiệp THPT năm 2011)
