Giải phương trình sau: 2cos2x – 3cosx + 1 = 0

Những câu hỏi liên quan
Giải phương trình sau: 2cos2x – 3cos x + 1 = 0
2cos2x – 3cosx + 1 = 0 (1)
đặt t = cosx, điều kiện –1 ≤ t ≤ 1
(1) trở thành 2t2 – 3t + 1 = 0
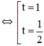 (thỏa mãn điều kiện).
(thỏa mãn điều kiện).
+ t = 1 ⇒ cos x = 1 ⇔ x = k.2π (k ∈ Z)
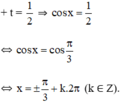
Vậy phương trình có tập nghiệm
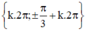 (k ∈ Z).
(k ∈ Z).
Đúng 0
Bình luận (0)
Giải các phương trình sau: 1 + sin x - cos x - sin 2 x + 2 cos 2 x = 0
1 + sin x - cos x - sin 2 x + 2 cos 2 x = 0 ( 1 ) T a c ó : 1 - sin 2 x = sin x - cos x 2 ⇔ 2 cos 2 x = 2 ( cos 2 x - sin 2 x ) = - 2 ( sin x - cos x ) ( sin x + cos x ) V ậ y ( 1 ) ⇔ ( sin x - cos x ) ( 1 + sin x - cos x - 2 sin x - 2 cos x ) = 0 ⇔ ( sin x - cos x ) ( 1 - sin x - 3 cos x ) = 0
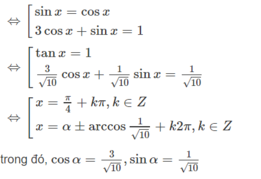
Đúng 0
Bình luận (0)
Giải các phương trình sau 5 sin 2 x + 3 cos x + 3 = 0
5 sin 2 x + 3 cos x + 3 = 0 ⇔ 5 ( 1 - cos 2 x ) + 3 cos x + 3 = 0 ⇔ 5 cos 2 x - 3 cos x - 8 = 0 ⇔ ( cos x + 1 ) ( 5 cos x - 8 ) = 0 ⇔ cos x = - 1 ⇔ x = ( 2 k + 1 ) π , k ∈ Z
Đúng 0
Bình luận (0)
a. 2cos2x – 3cosx + 1 = 0
2cos^2(x) - 3cosx + 1 = 0
<=> (cosx - 1)(2cosx - 1) = 0
TH1: cosx = 1 <=> x = k.2pi (k ∈ Z)
TH2: 2cosx = 1 <=> cosx = 1/2 <=> x = pi/3 + k.2pi (k ∈ Z)
Đúng 1
Bình luận (1)
Giải phương trình
2
cos
2
x
+
π
6
+
4
sin
x
cos
x
-
1
0
Đọc tiếp
Giải phương trình 2 cos 2 x + π 6 + 4 sin x cos x - 1 = 0
![]()
![]()
![]()
![]()
giải phương trình: 3cosx(1 - cos2x) + 2sin2x + sinx + cos2x = 0
cos2x = 1- sin^x
sin2x= 2sinxcosx
Nhóm lại bình thường và giải thôi
Đúng 0
Bình luận (0)
Giải phương trình sau: 2 cos 2 x - 3 sin 2 x + sin 2 x = 1
2 cos 2 x - 3 sin 2 x + sin 2 x = 1
- cosx = 0 thỏa mãn phương trình ⇒ phương trình có nghiệm x = π/2+kπ,k ∈ Z.
- Với cosx ≠ 0, chia hai vế cho cos 2 x , tìm được tanx = 1/6.
Vậy phương trình có các nghiệm x = π/2+kπ,k ∈ Z và x = arctan1/6 + kπ,k ∈ Z.
Đúng 0
Bình luận (0)
giải phương trình
sin^3x +2sin2x + 3cosx= 0
\(sin^3x+2sinx+3cosx=0\)
\(\Leftrightarrow sin^3x-sinx+3sinx+3cosx=0\)
\(\Leftrightarrow sinx\left(sin^2x-1\right)+3\left(sinx+cosx\right)=0\)
\(\Leftrightarrow-sinx.cosx+3\left(sinx+cosx\right)=0\)
\(\Leftrightarrow\dfrac{1-\left(sinx+cosx\right)^2}{2}+3\left(sinx+cosx\right)=0\)
\(\Leftrightarrow\left(sinx+cosx\right)^2-6\left(sinx+cosx\right)-1=0\)
\(\Leftrightarrow\left(sinx+cosx\right)^2-6\left(sinx+cosx\right)-1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx+cosx=3+\sqrt{10}\\sinx+cosx=3-\sqrt{10}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}sin\left(x+\dfrac{\pi}{4}\right)=\dfrac{3+\sqrt{10}}{\sqrt{2}}\left(l\right)\\sin\left(x+\dfrac{\pi}{4}\right)=\dfrac{3-\sqrt{10}}{\sqrt{2}}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{4}=arcsin\left(\dfrac{3-\sqrt{10}}{\sqrt{2}}\right)+k2\pi\\x+\dfrac{\pi}{4}=\pi-arcsin\left(\dfrac{3-\sqrt{10}}{\sqrt{2}}\right)+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+arcsin\left(\dfrac{3-\sqrt{10}}{\sqrt{2}}\right)+k2\pi\\x=\dfrac{3\pi}{4}-arcsin\left(\dfrac{3-\sqrt{10}}{\sqrt{2}}\right)+k2\pi\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Giá trị lớn nhất của hàm số
y
1
3
c
o
s
3
x
-
2
c
o
s
2
x
+
3
c
o
s
x
+
1
,
x thuộc
0
;
π
2
A. 1 B.
7
3
C. 2 D.
1
3
Đọc tiếp
Giá trị lớn nhất của hàm số y = 1 3 c o s 3 x - 2 c o s 2 x + 3 c o s x + 1 , x thuộc 0 ; π 2
A. 1
B. 7 3
C. 2
D. 1 3














