Cho hàm số y = x3 – 3x2 – 9x – 5. Phương trình y’ = 0 có nghiệm là:
A. {-1; 2}.
B. {-1; 3}.
C. {0; 4}.
D. {1; 2}.
Những câu hỏi liên quan
Cho hàm số y = x 3 - 3 x 2 - 9 x - 5 . Phương trình y' = 0 có nghiệm là
A. {-1;2}
B. {-1;3}
C. {0;4}
D. {1;2}
Cho hàm số
y
x
3
-
3
x
2
-
9
x
-
5
. Phương trình y 0 có nghiệm là: A.
-
1
;
2
B.
-
1
;
3
C.
0
;
4
D. ...
Đọc tiếp
Cho hàm số y = x 3 - 3 x 2 - 9 x - 5 . Phương trình y' = 0 có nghiệm là:
A. - 1 ; 2
B. - 1 ; 3
C. 0 ; 4
D. 1 ; 2
Cho hàm số y = x 3 − 3 x 2 − 9 x − 5 . Phương trình y ' = 0 có nghiệm là:
A.{-1;2}
B.{-1;3}
C. {0;4}
D.{1;2}
Chọn B.
Ta có y ' = 3 x 2 - 6 x - 9
y ' = 0 ⇔ 3 x 2 - 6 x - 9 = 0 ⇔ x = - 1 ; x = 3
Đúng 0
Bình luận (0)
Cho hàm số
y
-
x
3
+
3
x
2
-
2
có đồ thị như hình vẽ: Số nghiệm của phương trình
x
3
-
3
x
2
+
2...
Đọc tiếp
Cho hàm số y = - x 3 + 3 x 2 - 2 có đồ thị như hình vẽ:
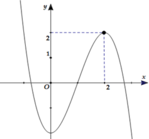
Số nghiệm của phương trình x 3 - 3 x 2 + 2 = 1 là
A. 3
B. 4
C. 6
D. 5
Đồ thị hình bên là của hàm số
y
-
x
3
+
3
x
2
-
4
. Để phương trình
x
3
-
3
x
2
+
m
0
có hai nghiệm phân biệt thì A. 0 m 4 B. m 4 C.
m
0...
Đọc tiếp
Đồ thị hình bên là của hàm số y = - x 3 + 3 x 2 - 4 . Để phương trình x 3 - 3 x 2 + m = 0 có hai nghiệm phân biệt thì
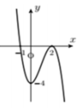
A. 0 < m < 4
B. m = 4
C. m = 0 hoặc m = 4
D. m = 0 hoặc m = - 4
Hàm số
y
x
3
−
3
x
2
+
1
có đồ thị như hình bên. Tất cả giá trị của thừa số m để phương trình
−
x
3
+
3
x
2
−
m
0
có ba nghiệm phân biệt là A.
0
≤
m
≤
4
B.
0...
Đọc tiếp
Hàm số y = x 3 − 3 x 2 + 1 có đồ thị như hình bên. Tất cả giá trị của thừa số m để phương trình − x 3 + 3 x 2 − m = 0 có ba nghiệm phân biệt là
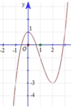
A. 0 ≤ m ≤ 4
B. 0 < m < 4
C. − 3 < m < 1
D. − 3 ≤ m ≤ 1
Đáp án B.
Ta có − x 3 + 3 x 2 − m = 0 ⇔ x 3 − 3 x 2 + 1 = 1 − m . Ta thấy số nghiệm của phương trình là số giao điểm của hai đồ thị hàm số y = x 3 − 3 x 2 + 1 và y = 1 − m .
Dựa vào đồ thị ta suy ra để cắt nhau tại 3 điểm thì − 3 < 1 − m < 1 ⇔ 0 < m < 4.
Đúng 0
Bình luận (0)
Cho hàm số y = f ( x ) = - x 3 - 3 x 2 + 9 x + 2011 có đồ thị (C). Giải bất phương trình: f'(x) ≤ 0.
Cho hàm số
y
-
x
3
-
3
x
2
+
4
có đồ thị (C) là hình vẽ dưới đây. Với giá trị nào của m thì phương trình
x
3
+
3
x
2
+
m
0
*
có hai nghiệm phân biệt? A. m 0 hoặc m 4 B. m -4 hoặ...
Đọc tiếp
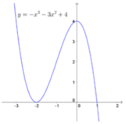
Cho hàm số y = - x 3 - 3 x 2 + 4 có đồ thị (C)
là hình vẽ dưới đây. Với giá trị nào của m thì phương trình x 3 + 3 x 2 + m = 0 *
có hai nghiệm phân biệt?
A. m = 0 hoặc m = 4
B. m = -4 hoặc m = 0
C. m = -2 hoặc m = 4
D. m = 0 hoặc m = 6
Cho hàm số
y
−
x
3
−
3
x
2
+
4
có đồ thị (C) là hình vẽ dưới đây. Với giá trị nào của m thì phương trình
x
3
+
3
x
2
+
m
0
∗
có hai nghiệm phân biệt? A. m 0 hoặc m 4 B. m 0 hoặc m 6 C. m -4 hoặc m 0 D. m -2...
Đọc tiếp
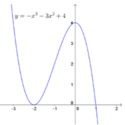
Cho hàm số y = − x 3 − 3 x 2 + 4 có đồ thị (C) là hình vẽ dưới đây. Với giá trị nào của m thì phương trình x 3 + 3 x 2 + m = 0 ∗ có hai nghiệm phân biệt?
A. m = 0 hoặc m = 4
B. m = 0 hoặc m = 6
C. m = -4 hoặc m = 0
D. m = -2 hoặc m = 4
