Trong không gian Oxyz, cho đường thẳng ∆ : x 2 = y - 1 1 = z - 2 - 1 và mặt cầu ( S ) : x 2 + y 2 + z 2 - 2 x + 4 z + 1 = 0 . Số điểm chung của ∆ và (S) là:
A. 3
B. 1
C. 2
D. 0
Trong không gian Oxyz, cho bốn đường thẳng d 1 : x - 3 1 = y + 1 - 2 = z + 1 1 ; d 2 : x 1 = y - 2 = z - 1 1 ; d 3 : x - 1 2 = y + 1 1 = z - 1 1 ; d 4 : x 1 = y - 1 - 1 = z - 1 1 . Số đường thẳng trong không gian cắt cả bốn đường thẳng trên là:
A. 0.
B. 2.
C. Vô số.
D. 1.
Chọn D
Đường thẳng d₁ đi qua điểm M₁ = (3;-1;-1) và có một véctơ chỉ phương là ![]()
Đường thẳng d₂ đi qua điểm M₂ = (0;0;1) và có một véctơ chỉ phương là ![]()
Do ![]() và M₁ ∉ d₁ nên hai đường thẳng d₁ và d₂ song song với nhau.
và M₁ ∉ d₁ nên hai đường thẳng d₁ và d₂ song song với nhau.
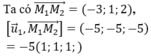
Gọi (α) là mặt phẳng chứa d₁ và d₂ khi đó (α) có một véctơ pháp tuyến là ![]() . Phương trình mặt phẳng (α) là x+y+z-1=0.
. Phương trình mặt phẳng (α) là x+y+z-1=0.
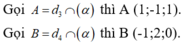
Do ![]() không cùng phương với
không cùng phương với ![]() nên đường thẳng AB cắt hai đường thẳng d₁ và d₂.
nên đường thẳng AB cắt hai đường thẳng d₁ và d₂.
Trong không gian Oxyz, cho bốn đường thẳng:
d 1 : x - 3 1 = y + 1 - 2 = z + 1 1 , d 2 : x 1 = y - 2 = z - 1 1 , d 3 : x - 1 2 = y + 1 1 = z - 1 1 , d 4 : x 1 = y - 1 - 1 = z - 1 1
Số đường thẳng trong không gian cắt cả bốn đường thẳng trên là:
A. 0.
B. 2.
C. Vô số.
D. 1.
Chọn D
Đường thẳng d1 đi qua điểm M1 (3; -1; -1) và có một véctơ chỉ phương là ![]()
Đường thẳng d2 đi qua điểm M2 (0; 0; 1) và có một véctơ chỉ phương là ![]()
Do ![]() và M1 ∉ d1 nên hai đường thẳng d1 và d2 song song với nhau.
và M1 ∉ d1 nên hai đường thẳng d1 và d2 song song với nhau.
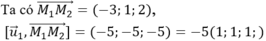
Gọi (α) là mặt phẳng chứa d1 và d2 khi đó (α) có một véctơ pháp tuyến là ![]()
Phương trình mặt phẳng (α) là x + y + z -1 = 0
Gọi A = d3 ∩ (α) thì A (1; -1; 1)
Gọi B = d4 ∩ (α) thì B (-1; 2; 0)
Do ![]() không cùng phương với
không cùng phương với ![]() nên đường thẳng AB cắt hai đường thẳng d1 và d2.
nên đường thẳng AB cắt hai đường thẳng d1 và d2.
Trong không gian tọa độ Oxyz, cho đường thẳng d: x - 1 2 = y + 1 - 1 = z + 2 - 2 . Điểm nào dưới đây KHÔNG thuộc đường thẳng d?
![]()
![]()
![]()
![]()
Thay lần lượt tọa độ các điểm vào phương trình đường thẳng ta thấy tọa độ của Q không thỏa mãn phương trình. Vậy điểm Q không thuộc đường thẳng d.
Chọn D
Trong không gian tọa độ Oxyz, cho đường thẳng d : x - 1 2 = y + 1 - 1 = z + 2 - 2 . Điểm nào dưới đây KHÔNG thuộc đường thẳng d?
A. M 3 ; - 2 ; - 4
B. 1 ; - 1 ; - 2
C. P - 1 ; 0 ; 0
D. Q - 3 ; 1 ; - 2
Đáp án D
Phương pháp:
Thay tọa độ các điểm vào phương trình đường thẳng và kiểm tra tọa độ đó có thỏa mãn phương trình hay không.
Cách giải
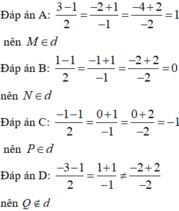
Trong không gian Oxyz, cho hai đường thẳng △ 1 : x - 1 - 2 = y + 2 1 = z - 3 2 và △ 2 : x + 3 1 = y - 1 1 = z + 2 - 4 . Góc giữa hai đường thẳng △ 1 , △ 2 bằng
A. 30 °
B. 45 °
C. 60 °
D. 135 °
Trong không gian Oxyz, cho mặt phẳng Oxyz và hai đường thẳng d 1 : x + 1 - 1 = y - 6 2 = z 1 và d 2 : x - 1 - 3 = y - 2 - 1 = z + 4 4 Đường thẳng vuông góc với (P) và cắt cả hai đường thẳng d 1 và d 2 có phương trình là
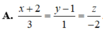
![]()
![]()
Trong không gian Oxyz, cho đường thẳng d : x - 2 - 1 = y - 1 2 = z 1 . Đường thẳng d có một vectơ chỉ phương là:
A. u 1 ⇀ = - 1 ; 2 ; 1
B. u 2 ⇀ = 2 ; 1 ; 0
C. u 3 ⇀ = 2 ; 1 ; 1
D. u 4 ⇀ = - 1 ; 2 ; 0
Trong không gian Oxyz , cho hai đường thẳng d1: x - 1 2 = y + 2 - 1 = z 1 và d2: x = 1 + 4 t y = - 1 - 2 t z = 2 + 2 t
Khoảng cách giữa hai đường thẳng đã cho bằng
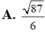
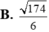
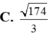
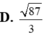
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: x - 3 2 = y + 2 - 1 = z + 1 4 . Điểm nào sau đây không thuộc đường thẳng
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho bốn đường thẳng
D 1 : x − 2 1 = y + 2 − 1 = z − 1 − 1 ; D 2 : x − 1 1 = y − 1 2 = z − 1 ; D 3 : x − 1 = y + 2 1 = z + 1 1
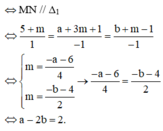
và đường thẳng D 4 : x − 5 1 = y − a 3 = z − b 1 . Biết không tồn tại đường thẳng nào trong không gian mà cắt được đồng thời cả bốn đường thẳng trên. Tính giá trị của biểu thức T = a - 2b.
A. T = -2
B. T = -3
C. T = 2
D. T = 3
Đáp án C.
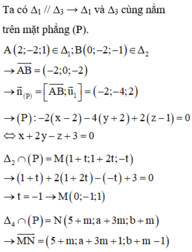
Không tồn tại đường thẳng nào trong không gian cắt cả 4 đường thẳng đã cho