Cho hình hộp chữ nhật ABCD.A'B'C'D' có diện tích đáy S A B C D = 24 c m 2 và có thể tích V = 84 c m 3 . Chiều cao của hình hộp chữ nhật có độ dài là?
A. h = 4( cm )
B. h = 3,5( cm )
C. h = 5( cm )
D. h = 2( cm )
Cho hình hộp chữ nhật ABCD.A'B'C'D' có đáy ABCD là hình vuông, chiều cao AA' = a và A ' C A ^ = 45 ° . Hãy tính:
a) Diện tích toàn phần hình hộp theo a;
b) Thể tích hình hộp theo a
Câu 1: Hình hộp chữ nhật có:
A. 6 cạnh B. 10 cạnh
C. 8 cạnh D. 12 cạnh
Câu 2: Hình hộp chữ nhật có:
A. 4 mặt B.5 mặt
C. 6 mặt D. 8 mặt
Câu 3: Tính diện tích mặt đáy của hình hộp chữ nhật hình có chiều dài a, chiều rộng b , chiều cao h ( cùng đơn vị đo) được tính theo công thức:
A. S = a+bx2 C. S = a x b
B. (a+b)x2 D. a: b
Câu 4: Diện tích xung quanh của hình hộp chữ nhật là diện tích của:
A. 2 mặt đáy
B. 4 mặt xung quanh
C. 2 mặt xung quanh
D. 6 mặt
Câu 5: Chu vi mặt đáy của hình hộp chữ nhật có chiều dài 1,5dm, chiều rộng 1,2dm chiều cao 1dm là:
A. 5,4dm B. 2,5dm
C. 2,7dm D. 5 dm
Câu 1: Hình hộp chữ nhật có:
A. 6 cạnh B. 10 cạnh
C. 8 cạnh D. 12 cạnh
Câu 2: Hình hộp chữ nhật có:
A. 4 mặt B.5 mặt
C. 6 mặt D. 8 mặt
Câu 3: Tính diện tích mặt đáy của hình hộp chữ nhật hình có chiều dài a, chiều rộng b , chiều cao h ( cùng đơn vị đo) được tính theo công thức:
A. S = a+bx2 C. S = a x b
B. (a+b)x2 D. a: b
Câu 4: Diện tích xung quanh của hình hộp chữ nhật là diện tích của:
A. 2 mặt đáy
B. 4 mặt xung quanh
C. 2 mặt xung quanh
D. 6 mặt
Câu 5: Chu vi mặt đáy của hình hộp chữ nhật có chiều dài 1,5dm, chiều rộng 1,2dm chiều cao 1dm là:
A. 5,4dm B. 2,5dm
C. 2,7dm D. 5 dm
Lời giải chi tiết: Chu vi mặt đáy là:
(1,5+1,2)×2=5,4(dm)
Đáp số: 5,4dm
Cho hình hộp chữ nhật ABCD.A'B'C'D' có diện tích đáy S A B C D = 24 c m 2 và có thể tích V = 84 c m 3 . Chiều cao của hình hộp chữ nhật có độ dài là?
A. h = 4( cm )
B. h = 3,5( cm )
C. h = 5( cm )
D. h = 2( cm )
Ta có: Thể tích cua hình hộp chữ nhật là
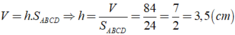
Vậy chiều cao của hình hộp chữ nhật là h = 3,5( cm )
Chọn đáp án B.
Cho hình hộp ABCD.A'B'C'D' có đáy là hình chữ nhật, hình chiếu của A' lên đáy (ABCD) trùng với trung điểm của cạnh AD. Biết rằng AB = a, AD = 2a và thể tích hình hộp đã cho bằng 2 a 3 . Khoảng cách từ B đến mặt phẳng (A'DCB') bằng:
A. 2 a 6 B. 2 a 3
C. 3 a 3 D. a 2
Chọn D.
Gọi H là trung điểm của cạnh AD. Kẻ HI vuông góc với A'D tại I. Khi đó d(B,(A'DCB')) = d(A,(A'DCB')) = 2d(H,(A'DCB')) = 2HI.
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = 12cm, AD = 16cm, AA' = 25cm.
a) Chứng minh rằng các tứ giác ACCA', BDD'B' là những hình chữ nhật.
b) Chứng minh rằng AC'2 = AB2 + AD2 + AA'2.
c) Tính diện tích toàn phần và thể tích của hình hộp chữ nhật.
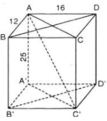
a) ABCD.A’B’C’D’ là hình hộp chữ nhật
⇒ AA’ // CC’, AA’ = CC’
⇒ AA’C’C là hình bình hành
Lại có : AA’ ⊥ (ABCD) ⇒ AA’ ⊥ AC ⇒ 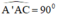
⇒ Hình bình hành AA’C’C là hình chữ nhật.
Chứng minh tương tự được tứ giác BDD'B' là những hình chữ nhật
b) Áp dụng định lý Pytago:
Trong tam giác vuông ACC’ ta có:
AC’2 = AC2 + CC’2 = AC2 + AA’2
Trong tam giác vuông ABC ta có:
AC2 = AB2 + BC2 = AB2 + AD2
Do đó: AC’2 =AB2 + AD2 + AA’2.
c) Hình hộp chữ nhật được xem như hình lăng trụ đứng.
Diện tích xung quanh:
Sxq = 2.(AB + AD).AA’
= 2.(12 + 16).25
= 1400 (cm2 )
Diện tích một đáy:
Sđ = AB.AD
= 12.16
= 192 (cm2 )
Diện tích toàn phần:
Stp = Sxq + 2Sđ
= 1400 + 2.192
= 1784 (cm2 )
Thể tích:
V = AB.AD.AA’
= 12.16.25
= 4800 (cm3 )
Cho hình hộp chữ nhật ABCD.A'B'C'D' có đáy ABCD là hình vuông, AB=20cm, AA'=19,4cm.
a) Chứng minh tứ giác ABC'D', CDA'B' là hình chũ nhật
b) Tính thể tích và diện tích toàn phần của hình hộp.
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB=a, AA'=2a Biết thể tích hình cầu ngoại tiếp tứ diện ABCD' là 9 π a 3 2 Tính thể tích V của hình hộp chữ nhật ABCD.A'B'C'D'.
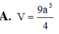
![]()
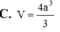
![]()
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, AA' = 2a. Biết thể tích hình cầu ngoại tiếp tứ diện ABCD' là 9 πa 3 2 . Tính thể tích V của hình hộp chữ nhật ABCD.A'B'C'D'.
A. V = 9 a 3 4
B. V = 4 a 3
C. V = 4 a 3 3
D. V = 2 a 3
Đáp án B
Thể tích khối cầu ngoại tiếp tứ diện ABCD’ chính là thể tích khối cầu ngoại tiếp hình hộp chữ nhật ABCD.A’B’C’D’. Khi đó, bán kính khối cầu ngoại tiếp là R = A C ' 2 .
Ta có V = 4 3 πR 3 = 4 3 π . AC ' 3 8 = 9 2 πa 3 ⇒ AC ' 3 = 27 a 3 ⇒ AC ' = 3 a .
Mặt khác A C ' 2 = A B 2 + A D 2 + A A ' 2 ⇒ A D 2 = ( 3 a 2 ) - a 2 - ( 2 a ) 2 = 4 a 2 ⇒ A D = 2 a .
Vậy thể tích của hình hộp chữ nhật ABCD.A'B'C'D' là V = A A ' . A B . A D = a . 2 a . 2 a = 4 a 3 .
Cho hình hộp chữ nhật ABCD.A'B'C'D' như hình vẽ. Cắt hình hộp theo mặt cắt MNPQ với M là trung điểm của AB và (MNPQ) song song (AA'D'D).
a) Chứng minh NQ// (BCC'B')
b) Nêu vị trí tương đối của các cặp đường thẳng AN và BD; PB' và MN.
c) Cho AA' = 50cm và ND' = DM = 50 2 c m . Khi đó AMND.A'QPD' là hình gì?
d) Tính diện tích xung quanh của hình hộp chữ nhật ABCD.A'B'C'D'.
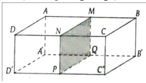
a) NQ//DA'// (BCC'B')
b) AN và BD cắt nhau, PB' và MN chéo nhau.
c) AMND.A'QPD' là hình lập phương
d) Diện tích xung quanh của hình hộp là 15000cm2
