Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, A B = B C = 1 2 A D = 2 a . Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Thể tích khối chóp S.ACD.
A. 4 a 3 3 3
B. a 3 3 3
C. a 3 2 6
D. a 3 3 6
Những câu hỏi liên quan
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, ABBC2, AD3. Cạnh bên SA2 và vuông góc với đáy. Tính thể tích khối chóp S.ABCD. A.
V
4
B.
V
10
3
C.
V
10
3
3
D.
V
17
6
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, AB=BC=2, AD=3. Cạnh bên SA=2 và vuông góc với đáy. Tính thể tích khối chóp S.ABCD.
A. V = 4
B. V = 10 3
C. V = 10 3 3
D. V = 17 6
Đáp án B
Diện tích hình thang ABCD là:
S A B C D = A B . A D + B C 2 = 5
Vậy thể tích khối chóp S.ABCD là:
V = 1 3 . S A . S A B C D = 1 3 . S A . S A B C D = 1 3 .2.5 = 10 3 (đvtt)
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A,B với AB=BC=a , AD=2a , SA vuông góc (ABCD) và SA = a√2 a) Cminh các mặt bên của hình chóp là các tam giác vuông
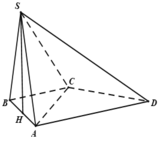
Cho hình chóp S.ABCD có đường thẳng SA vuông góc với mặt phẳng (ABCD), đáy ABCD là hình thang vuông tại A và B, có
A
B
a
,
A
D
2
a
,
B
C
a
. Biết rằng
S
A
a
2
. Tính thể tích V của khối chóp S.ABCD theo a.
Đọc tiếp
Cho hình chóp S.ABCD có đường thẳng SA vuông góc với mặt phẳng (ABCD), đáy ABCD là hình thang vuông tại A và B, có A B = a , A D = 2 a , B C = a . Biết rằng S A = a 2 . Tính thể tích V của khối chóp S.ABCD theo a.
Cho hình chóp S.ABCD có đường thẳng SA vuông góc với mặt phẳng (ABCD), đáy ABCD là hình thang vuông tại A và B, có
A
B
a
,
A
D
2
a
,
B
C
a
.
Biết rằng
S
A
a
2
Tính thể tích V của khối chóp S.ABCD theo a. A.
V
a
3...
Đọc tiếp
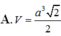
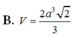
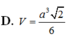
Cho hình chóp S.ABCD có đường thẳng SA vuông góc với mặt phẳng (ABCD), đáy ABCD là hình thang vuông tại A và B, có A B = a , A D = 2 a , B C = a . Biết rằng S A = a 2 Tính thể tích V của khối chóp S.ABCD theo a.
A. V = a 3 2 2
B. V = 2 a 3 2 3
C. V = 2 a 2 3
D. V = a 3 2 6
Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng (ABCD), đáy là hình thang ABCD vuông tại A và B có AB a, AD 3a, BCa. Biết SA
a
3
, tính thể tích khối chóp S.BCD theo a. A.
2
3
a
3
B.
3
a
3
6
C.
2...
Đọc tiếp
Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng (ABCD), đáy là hình thang ABCD vuông tại A và B có AB = a, AD = 3a, BC=a. Biết SA = a 3 , tính thể tích khối chóp S.BCD theo a.
A. 2 3 a 3
B. 3 a 3 6
C. 2 3 a 3 3
D. 3 a 3 4
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, ABBC
1
2
ADa. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ACD. A.
V
a
3
3
B.
V
a
3
2
C.
V...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, AB=BC= 1 2 AD=a. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ACD.
A. V = a 3 3
B. V = a 3 2
C. V = a 3 2 6
D. V = a 3 3 6
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Hình chiếu vuông góc của S trên mặt đáy (ABCD) trùng với trung điểm AB. Biết ABa, BC2a, BDa
10
. Góc giữa hai mặt phẳng (SBD) và mặt phẳng đáy là
60
0
. Tính thể tích V của khối chóp S.ABCD theo a.
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Hình chiếu vuông góc của S trên mặt đáy (ABCD) trùng với trung điểm AB. Biết AB=a, BC=2a, BD=a 10 . Góc giữa hai mặt phẳng (SBD) và mặt phẳng đáy là 60 0 . Tính thể tích V của khối chóp S.ABCD theo a.
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Hình chiếu vuông góc của S trên mặt đáy (ABCD) trùng với trung điểm AB. Biết AB a, BC 2a, BD a
10
. Góc giữa hai mặt phẳng (SBD) và mặt phẳng đáy là 600. Tính thể tích V của khối chóp S.ABCD theo a A.
V
3
30
a...
Đọc tiếp
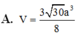
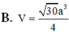
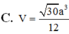
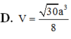
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Hình chiếu vuông góc của S trên mặt đáy (ABCD) trùng với trung điểm AB. Biết AB = a, BC = 2a, BD = a 10 . Góc giữa hai mặt phẳng (SBD) và mặt phẳng đáy là 600. Tính thể tích V của khối chóp S.ABCD theo a
A. V = 3 30 a 3 8
B. V = 30 a 3 4
C. V = 30 a 3 12
D. V = 30 a 3 8
Đáp án D
Dựng HK ⊥ BD, do SH ⊥ BD nên ta có:
(SKH) ⊥ BD => Góc giữa hai mặt phẳng (SBD) và mặt phẳng đáy là góc SKH = 600
Lại có: 
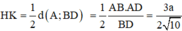
Do đó 
Vậy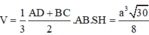 
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Hình chiếu vuông góc của S trên mặt đáy (ABCD) trùng với trung điểm AB. Biết AB a, BC 2a, BD a
10
. Góc giữa hai mặt phẳng (SBD) và mặt phẳng đáy là 600. Tính thể tích V của khối chóp S.ABCD theo a. A. V
3
30
a
3
8
B. V...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Hình chiếu vuông góc của S trên mặt đáy (ABCD) trùng với trung điểm AB. Biết AB = a, BC = 2a, BD = a 10 . Góc giữa hai mặt phẳng (SBD) và mặt phẳng đáy là 600. Tính thể tích V của khối chóp S.ABCD theo a.
A. V = 3 30 a 3 8
B. V = 30 a 3 4
C. V = 30 a 3 12
D. V = 30 a 3 8
Chọn D
Ta có 
Gọi H là trung điểm AB thì 
,
kẻ 
, ta có 
là góc giữa (SBD) và (ABCD), do đó 
= 600
Gọi AM là đường cao của tam giác vuông ABD. Khi đó, ta có:
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có SA vuông góc với đáy;
S
A
a
6
.
Đáy ABCD là hình thang vuông tại A và B,
A
B
B
C
1
2
A
D
a
.
Gọi E là trung điểm AD. Tính bán kính mặt cầu ngoại tiếp hình chóp S.ECD A.
R
a
30...
Đọc tiếp
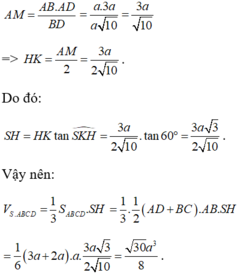
Cho hình chóp S.ABCD có SA vuông góc với đáy; S A = a 6 . Đáy ABCD là hình thang vuông tại A và B, A B = B C = 1 2 A D = a . Gọi E là trung điểm AD. Tính bán kính mặt cầu ngoại tiếp hình chóp S.ECD
A. R = a 30 3
B. R = a 19 6
C. R = a 6
D. R = 114 6 a .
