Tìm m để đồ thị hàm số y = x 2 - 9 x cắt đường thẳng y = m tại bốn điểm phân biệt.
A. m > 0
B. m > - 81 4
C. - 81 4 < m < 0
D. m < -3
Biết S = (a,b) là tập hợp tất cả các giá trị của tham số m để đường thẳng y = m cắt đồ thị hàm số y = | \(x^2-4x+3\) | tại bốn điểm phân biệt . Tìm a + b
Có bao nhiêu giá trị nguyên của tham số m để đường thẳng y=m(x-4) cắt đồ thị của hàm số y = x 2 − 1 x 2 − 9 tại bốn điểm phân biệt?
A. 1
B. 5
C. 3
D. 7
a) lập bảng biến thiên và vẽ đồ thị hàm số y = x\(^2\)+3x+2
b) tìm m để đường thẳng y = -x+m cắt (P) tại 2 điểm phân biệt có hoành độ dương
c) tìm m để đường thẳng y = -2x+3m cắt (P) tại 2 điểm phân biệt có hoành độ x1, x2 thỏa mãn x\(_1\)= 3x\(_2\)
Có bao nhiêu số thực m để đường thẳng y=-x+m cắt đồ thị hàm số y = 1 3 x 3 + 2 - m x 2 + 3 2 m - 3 x + m tại ba điểm phân biệt A(0;m), B, C sao cho đường thẳng OA là phân giác của góc BOC.
A. 1.
B. 3.
C. 2.
D. 0.
Tìm m để đường thẳng y=m(x+1)-2 cắt đồ thị hàm số y = x 3 + 3 x 2 - 4 tại ba điểm phân biệt
A. m>3
B. m<3
C. m>-3
D. m<-3
Tìm m để đường thẳng y = x + m cắt đồ thị hàm số y = 2 x x + 1 tại hai điểm phân biệt.
A. m ∈ ( - ∞ ; 2 - 2 2 ) ∪ ( 3 + 3 2 ; + ∞ )
B. m ∈ ( - ∞ ; 4 - 2 2 ) ∪ ( 4 + 2 ; + ∞ )
C. m ∈ ( - ∞ ; 1 - 2 3 ) ∪ ( 1 + 2 3 ; + ∞ )
D. m ∈ ( - ∞ ; 3 - 2 2 ) ∪ ( 3 + 2 2 ; + ∞ )
Tìm m để đường thẳng d : y = x - m cắt đồ thị hàm số ( C ) : y = x + 1 x - 1 tại hai điểm phân biệt A, B sao cho A B = 3 2
A. m = 2 và m = -2
B. m = 4 và m = -4
C. m = 1 và m = -1
D. m = 3 và m = -3
Tìm m để đường thẳng d : y = x - m cắt đồ thị hàm số C : y = x + 1 x - 1 tại hai điểm phân biệt A, B sao cho A B = 3 2
A. m = 2 và m = -2
B. m = 4 và m = -4
C. m = 1 và m = -1
D. m = 3 và m = -3
Chọn C.
Phương pháp: Sử dụng phương trình hoành độ giao điểm và định lý Viet.
Cách giải: Phương trình hoành độ giao điểm là

Vì a,c là nghiệm của (*) nên theo định lý Viet ta có:
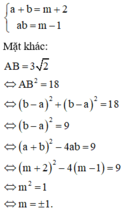
cho hàm số \(y=2x^2-6x-m+1\) (*) với m là tham số
a, Khi m=9 tìm x để y=0
b. Tìm m để đường thẳng y=x+1 cắt đồ thị (*) tại 2 điểm phân biệt và tìm tọa độ trung điểm của đoạn thẳng nối 2 giao điểm đó.