Với giá trị nào của m thì hai đường thẳng d1: 2x- 3y -10= 0 và d 2 : x = 2 - 3 t y = 1 - 4 m t vuông góc nhau ?
![]()
![]()
![]()
![]()
Với giá trị nào của m thì hai đường thẳng d1: 2x - 3y + 1 = 0 và d 2 : x = 1 + 2 t y = 7 - m t vuông góc với nhau?
A. m = 3 2
B. m = 3
C. m = -3
D. m = - 3 2
Với giá trị nào của m thì hai đường thẳng d 1 : x = 2 + 2 t y = 1 + m t và d2 : 4x – 3y + m= 0 trùng nhau ?
A.m= 1
B.m= -1
C.m= 2
D.không có m thỏa mãn
Đáp án D
Để 2 đường thẳng đã cho trùng nhau khi và chỉ khi:
Hệ phương trình
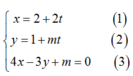 có vô số nghiệm.
có vô số nghiệm.
Thay (1) ; (2) vào (3) ta được : 4 (2+ 2t) -3 (1+ mt) + m= 0
Hay ( 3m- 8)t = m+5 (*)
Phương trình (*) có vô số nghiệm khi và chỉ khi
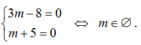
Với giá trị nào của m thì hai đường thẳng d1: 4x -3y + 3m= 0 và d 2 : x = 1 + 2 t y = 4 + m t trùng nhau ?
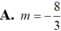

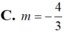
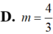

Thay (1) ; (2) vào (3) ta được 4( 1+ 2t) -3( 4+ mt) + 3m = 0
Hay ( 3m- 8) t= 3m- 8 (*)
Phương trình (*) có nghiệm tùy ý khi và chỉ khi 3m- 8= 0 hay m= 8/3.
Chọn B.
với giá trị nào của m thì hai đường thẳng d1:2x+y+4-m=0 và d2:(m+3)x+y+2m-1=0
Thì hai đường thẳng thế nào hả bạn?
Với giá trị nào của m thì hai đường thẳng (∆1) : 2x- 3y - m= 0 và ( ∆ 2 ) : x = 2 = 2 t y = 1 + m t trùng nhau?
A. Không có m
B.m= -2
C. m = 4/3
D.m= 1
Đáp án A
Gọi M( 2+2t; 1+ mt) là điểm tùy ý thuộc ∆2
Để M nằm trên ∆1 khi và chi khi:
2( 2+ 2t) -3( 1+ mt) - m= 0 hay t( 4-3m) + 1- m= 0 n(*) luôn đúng với mọi t.
∆ 1 ≡ ∆ 2 ⇔ ( * ) thỏa với mọi t ⇔ 4 - 3 m = 0 1 - m = 0 (vô nghiệm)
Vậy không có m thỏa yêu cầu bài toán.
Với giá trị nào của m thì hai đường thẳng d1: 3x+ 4y+ 10= 0 và d2: (2m-1) x+ m2y + 10= 0 trùng nhau ?
A. m ∈ ∅
B.m= -2
C.m= 2
D.mọi m
Để 2 đường thẳng đã cho trùng nhau khi và chỉ khi
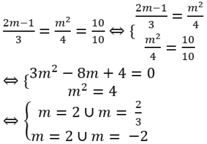
Tương đương m= 2.
Chọn C.
1.a) Với giá trị nào của m thì hai đường thẳng y= 2x + 3 + m và y= 3x + 5 - m, cắt nhau tại một điểm trên trục tung
b) Viết phương trình đường thẳng (d) biết (d) song song với (d'): y = \(\dfrac{-1}{2}x\) và cắt trục hoành tại điểm có hoành độ bằng 10
2. Cho các đường thẳng (d1): y= 4mx - (m + 5) với (m\(\ne\)0)
(d2): y= (3m + 1) x + (m - 9)
a) Với giá trị nào của m thì ( d1) // (d2)
b) Với giá trị nào của m thì (d1) cắt (d2). Tìm tọa độ giao điểm khi m = 2
Bài 1)
a) Xét phương trình hoành độ giao điểm: \(2x+3+m=3x+5-m\)
\(\Leftrightarrow x=3+m+m-5\Leftrightarrow x=2m-2\)
Để giao điểm của hai đường thẳng trên nằm trên trục tung thì \(2m-2=0\Leftrightarrow m=1\)
b) Do (d) // (d') nên (d) có phương trình \(y=-\frac{1}{2}x+b\)
Do (d) cắt trục hoành tại điểm có hoành độ x = 10 nên điểm (10;0) thuộc đường thẳng (d0.
Vậy thì \(0=-\frac{1}{2}.10+b\Leftrightarrow b=5\)
Vậy phương trình đường thẳng (d) là \(y=-\frac{1}{2}x+5\)
Bài 2)
a) Để (d1)//(d2) thì \(4m=3m+1\Leftrightarrow m=1\)
b) Để (d1)//(d2) thì \(4m\ne3m+1\Leftrightarrow m\ne1\)
Khi m = 2, ta có phương trình hoành độ giao điểm là:
\(8x-7=7x-7\Leftrightarrow x=0\)
Với \(x=0,y=-7\)
Vậy tọa độ giao điểm của (d1) và (d2) là (0; -7)
Với giá trị nào của m thì hai đường thẳng d: 2x + ( m 2 +1)y - 3 = 0 và d': x + my - 10 = 0 song song?
A. m = 1 hoặc m = 2
B. m = 1 hoặc m = 0
C. m = 2
D. m = 1
Đáp án: D
Để hai đường thẳng d: 2x + ( m 2 + 1)y - 3 = 0 và d': x + my - 10 = 0 song song thì:
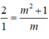
⇒ 2m = m 2 + 1 ⇔ m 2 - 2m + 1 = 0 ⇔ (m - 1 ) 2 = 0 ⇔ m = 1
Vậy với m = 1 thì d và d’ song song với nhau.
với giá trị nào của m thì đường thẳng d1:2x+y+4-m=0 và d2:(m+3)x+y+2m-1=0 song song?
Để hai đường song song thì m+3=2 và 2m-1<>4-m
=>m=-1 và 3m<>5
=>m=-1