Tìm tập xác định của hàm số
Đọc tiếp
Tìm tập xác định của hàm số 
Những câu hỏi liên quan
I. HÀM SỐ, TXĐ, CHẴN LẺ, ĐƠN ĐIỆU, ĐỒ THỊ.1. TXĐ CỦA HÀM SỐCâu 1.Tìm tập xác định của hàm số ydfrac{sqrt{x-1}}{x-3}Câu 2.Tìm tập xác định của hàm số y sqrt[3]{x-1}Câu 3. Tìm tập xác định của hàm số ydfrac{sqrt[3]{1-x}+3}{sqrt{x+3}}Câu 4. Tìm tập xác định của hàm số ysqrt{left|x-2right|}
Đọc tiếp
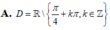
I. HÀM SỐ, TXĐ, CHẴN LẺ, ĐƠN ĐIỆU, ĐỒ THỊ.
1. TXĐ CỦA HÀM SỐ
Câu 1.Tìm tập xác định của hàm số y=\(\dfrac{\sqrt{x-1}}{x-3}\)
Câu 2.Tìm tập xác định của hàm số y= \(\sqrt[3]{x-1}\)
Câu 3. Tìm tập xác định của hàm số y=\(\dfrac{\sqrt[3]{1-x}+3}{\sqrt{x+3}}\)
Câu 4. Tìm tập xác định của hàm số y=\(\sqrt{\left|x-2\right|}\)
ĐKXĐ:
a. \(\left\{{}\begin{matrix}x-1\ge0\\x-3\ne0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x\ge1\\x\ne3\end{matrix}\right.\) \(\Rightarrow D=[1;+\infty)\backslash\left\{3\right\}\)
b. \(D=R\)
c. \(x+3>0\Rightarrow x>-3\Rightarrow D=\left(-3;+\infty\right)\)
d. \(\left|x-2\right|\ge0\Rightarrow x\in R\Rightarrow D=R\)
Đúng 1
Bình luận (0)
y= \(\dfrac{mx}{\sqrt{x-m+2}+1}\)
a, Tìm tập xác định của hàm số theo tham số m
b, Tìm m để hàm số có tập xác định trên (0;1)
Gọi tập xác định là D. Tìm tập xác định của hàm số
y
x
2
x
-
x
2
-
1
A.
D
R
/
0
,
1
B.
D...
Đọc tiếp
Gọi tập xác định là D. Tìm tập xác định của hàm số y = x 2 x - x 2 - 1
A. D = R / 0 , 1
B. D = R / 1
C. D = R / 0
D. D=(0,1)
Xét bốn mệnh đề sau:
1
: Hàm số
y
s
inx
có tập xác định là
R
2
: Hàm số
y
c
osx
có tập xác định là
R
3
Hàm số
y
tan
x
có tập xác định là
R
4
Hàm số
y
cot...
Đọc tiếp
Xét bốn mệnh đề sau:
1 : Hàm số y = s inx có tập xác định là R
2 : Hàm số y = c osx có tập xác định là R
3 Hàm số y = tan x có tập xác định là R
4 Hàm số y = cot x có tập xác định là R
Tìm số phát biểu đúng.
A. 3
B. 2
C. 4
D. 1
Đáp án là B
• Hàm số y = sin x ; y = cos x có tập xác định D = ℝ .
• Hàm số y = tan x & y = cot x có tập xác định lần lượt D = ℝ \ π 2 + k π ; D = ℝ \ k π .
Đúng 0
Bình luận (0)
Cho hàm số
y
2
x
-
1
3
. Tìm tập xác định của hàm số A.
1
;
+
∞
B.
1
2
;
+
∞...
Đọc tiếp
Cho hàm số y = 2 x - 1 3 . Tìm tập xác định của hàm số
A. 1 ; + ∞
B. 1 2 ; + ∞
C. ℝ \ 1 2
D. 1 2 ; + ∞
Cho hàm số
y
2
x
-
1
3
. Tìm tập xác định của hàm số
Đọc tiếp
Cho hàm số y = 2 x - 1 3 . Tìm tập xác định của hàm số
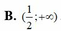
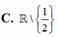
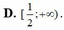
Cho hàm số y=\(\sqrt{2-x+2\sqrt{1}-x}\)
1,tìm tập xác định của hàm số
2,xét hàm số đồng biến,nghịch biến trên tập xác định của nó
Cho hàm số : \(y=\sqrt{x+1}\)
a/ Tìm tập xác định của hàm số
b/ Hỏi hàm số trên đồng biến hay nghịch biến trên tập xác định của nó.
Tìm tập xác định của hàm số
ĐKXĐ:
a. \(x-1\ne0\Rightarrow x\ne1\)
b. \(sinx+1>0\Rightarrow sinx\ne-1\Rightarrow x\ne-\dfrac{\pi}{2}+k2\pi\)
c. \(cos\left(2x-\dfrac{\pi}{6}\right)\ne0\Rightarrow2x-\dfrac{\pi}{6}\ne\dfrac{\pi}{2}+k\pi\Rightarrow x\ne\dfrac{\pi}{3}+\dfrac{k\pi}{2}\)
d. \(cos\left(3x-\pi\right)\ne0\Rightarrow cos3x\ne0\Rightarrow3x\ne\dfrac{\pi}{2}+k\pi\Rightarrow x\ne\dfrac{\pi}{6}+\dfrac{k\pi}{3}\)
e. \(sin^2x-cos^2x\ne0\Rightarrow cos2x\ne0\Rightarrow2x\ne\dfrac{\pi}{2}+k\pi\Rightarrow x\ne\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
g. \(cos2x-1\ne0\Rightarrow cos2x\ne1\Rightarrow2x\ne k2\pi\Rightarrow x\ne k\pi\)
Đúng 1
Bình luận (0)