Giúp em với ạ! Em cám ơn

Những câu hỏi liên quan

Mọi người giúp em từ câu b với ạ giúp em trc 6h30 với ạ em cám ơn
a) Xét ΔMNI vuông tại M và ΔHPI vuông tại P có
\(\widehat{MIN}=\widehat{HIP}\)(hai góc đối đỉnh)
Do đó: ΔMNI\(\sim\)ΔHPI(g-g)
Đúng 1
Bình luận (0)
b) Ta có: ΔMNI\(\sim\)ΔHPI(cmt)
nên \(\widehat{MNI}=\widehat{HPI}\)(hai góc tương ứng)
hay \(\widehat{MNI}=\widehat{MPK}\)
Xét ΔMNI vuông tại M và ΔMPK vuông tại M có
\(\widehat{MNI}=\widehat{MPK}\)(cmt)
Do đó: ΔMNI\(\sim\)ΔMPK(g-g)
Suy ra: \(\dfrac{MN}{MP}=\dfrac{MI}{MK}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(\dfrac{MN}{MI}=\dfrac{MP}{MK}\)
Xét ΔMNP vuông tại M và ΔMIK vuông tại M có
\(\dfrac{MN}{MI}=\dfrac{MP}{MK}\)(cmt)
Do đó: ΔMNP\(\sim\)ΔMIK(c-g-c)
Đúng 1
Bình luận (0)
Mọi người giúp em với ạ, em cám ơn ạ!!


Giúp em với ạ. Em cám ơn

Giúp em với ạ . Em cám ơn

Giúp em bài này với ạ. Em cám ơn ạ 🤭
Hello! John.
OK. So we'll go on a sightseeing tour by bikes at weekend
Đúng 3
Bình luận (0)
Giúp em bài này với ạ. Em cám ơn ạ 😆
Câu 4:
4.1/ Ta có: \(n_{NaCl}=2,5.0,4=1\left(mol\right)\)
\(\Rightarrow m_{NaCl}=1.58,5=58,5\left(g\right)\)
4.2/ Ta có: \(n_{Zn}=\dfrac{13}{65}=0,2\left(mol\right)\)
a, PT: \(Zn+2HCl\rightarrow ZnCl_2+H_2\)
_____0,2___________0,2____0,2 (mol)
b, \(V_{H_2}=0,2.22,4=4,48\left(l\right)\)
c, \(m_{ZnCl_2}=0,2.136=27,2\left(g\right)\)
Bạn tham khảo nhé!
Đúng 1
Bình luận (0)
GIÚP EM CÂU C BÀI 1 VỚI Ạ,EM CÁM ƠN Ạ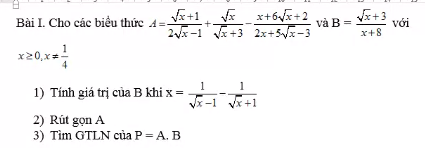

GIÚP EM CÂU B VỚI Ạ, EM CÁM ƠN
a)\(R_{23}=R_2+R_3=2+4=6\Omega\)
\(R_{123}=\dfrac{R_1\cdot R_{23}}{R_1+R_{23}}=\dfrac{2\cdot6}{2+6}=1,5\Omega\)
\(R_{tđ}=R_4+R_{123}=4,4+1,5=5,9\Omega\)
\(I_m=\dfrac{\xi}{r+R_N}=\dfrac{12}{0,1+5,9}=2A\)
\(U_{AB}=2\cdot5,9=11,8V\)
b)\(I_4=I_{123}=I_m=2A\)
\(U_1=U_{23}=U_{123}=2\cdot1,5=3V\)
\(I_1=\dfrac{U_1}{R_1}=\dfrac{3}{2}=1,5A\)
\(I_2=I_3=I_{23}=\dfrac{U_{23}}{R_{23}}=\dfrac{3}{6}=0,5A\)
\(U_{AC}=U_4+U_2=I_4\cdot R_4+I_2\cdot R_2=2\cdot4,4+0,5\cdot2=9,8V\)
Đúng 1
Bình luận (0)
giúp em bài này với ạ. em cám ơn
\(\dfrac{2020}{2019}>\dfrac{2019}{2020}\Rightarrow0< a< 1\)
\(log_ba< 1\Rightarrow b>1\)
\(P=log_b^2a+log_b^22-\dfrac{m^2log_2b}{log_2a}+2\left(log_ba-2log_b2\right)-\dfrac{4^{ab^2}-2m.2^{ab^2}}{log_ba}\)
\(=log_b^2a+log_b^22+2log_ba-4log_b2-\dfrac{4^{ab^2}-2m.2^{ab^2}+m^2}{log_ba}\)
\(=\left(log_ba+1\right)^2+\left(log_b2-2\right)^2+\dfrac{\left(2^{ab^2}-m\right)^2}{-log_ba}-5\ge-5\)
Dấu "=" xảy ra khi: \(\left\{{}\begin{matrix}log_ba=-1\\log_b2=2\\2^{ab^2}=m\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{\sqrt{2}}\\b=\sqrt{2}\\m=2^{ab^2}=2^{\sqrt{2}}\end{matrix}\right.\)
Sau khi tính lại thì không có đáp án nào đúng :(
Đúng 3
Bình luận (0)




















