Gọi z 0 là nghiệm phức có phần ảo âm của phương trình z 2 + 2 z + 5 = 0 . Trên mặt phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn số phức w = i 2019 z 0 ?
A. M(-2; 1)
B. M(2; 1)
C. M(-2; -1)
D. M(2; -1)
Gọi z1 z2 là các nghiệm phức của phương trình \(z^2+4z+7=0\) . Số phức \(z_1.\overline{z_2}+\overline{z_2}.z_1\) bằng
A:2
B:10
C:2i
D:10i
Chắc bạn ghi nhầm đề \(z_1\overline{z_2}+\overline{z_1}z_2\) mới có lý chứ nhỉ?
Khi pt bậc 2 có 2 nghiệm phức \(z_1;z_2\) thì \(z_1=\overline{z_2}\)
Do đó \(z_1\overline{z_2}+\overline{z_1}z_2=z_1^2+z_2^2=\left(z_1+z_2\right)^2-2z_1z_2=\left(-4\right)^2-2.7=2\)
Gọi z1 z2 là hai nghiệm phức của phương trình \(z^2-4z+5=0\) . Tính:
w = \(\dfrac{1}{z_1}+\dfrac{1}{z_2}+i\left(z_1^2z_2+z^2_2z_1\right)\)
\(z^2-4z+5=0\Rightarrow\left\{{}\begin{matrix}z_1+z_2=4\\z_1z_2=5\end{matrix}\right.\) theo hệ thức Viet
\(w=\dfrac{z_1+z_2}{z_1z_2}+i.z_1z_2\left(z_1+z_2\right)=\dfrac{4}{5}+i.5.4=\dfrac{4}{5}+20i\)
Gọi z1 , z2 là hai nghiệm phức của phương trình \(z^2-4z+5=0\) . Giá trị của biểu thức \(\left(z_1-1\right)^{2019}+\left(z_2-1\right)^{2019}\) bằng?
A: 21009
B: 21010
C:0
D: -21010
\(\Delta'=4-5=-1\Rightarrow\left[{}\begin{matrix}z_1=2+i\\z_2=2-i\end{matrix}\right.\)
\(\Rightarrow\left(z_1-1\right)^{2019}+\left(z_2-1\right)^{2019}=\left(i+1\right)^{2019}+\left(i-1\right)^{2019}\)
\(=\left(i+1\right)\left[\left(i+1\right)^2\right]^{1009}+\left(i-1\right)\left[\left(i-1\right)^2\right]^{1009}\)
\(=\left(i+1\right)\left(2i\right)^{1009}+\left(1-i\right)\left(-2i\right)^{1009}=\left(2i\right)^{1009}\left(i+1+i-1\right)=\left(2i\right)^{1009}.2i=\left(2i\right)^{1010}=-2^{1010}\)
=>D
P/s: Sry nó bị trôi thông báo nên toi ko để ý
Cho số phức z = 1 + 2 i 2 - i . Phần thực và phần ảo của số phức w = (z + 1)(z + 2) là
A. 2 và 1
B. 1 và 3
C. 2 và i
D. 1 và 3i
Ta có
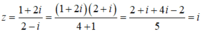
Suy ra w = (z + 1)(z + 2) = (i + 1)(i + 2) = -1 + 2i + i + 2 = 1 + 3i
Chọn B
Phần thực và phần ảo của số phức z thỏa mãn (1 - i)z - 1 + 5i = 0 là
A. 3 và –2
B. 3 và 2
C. 3 và – 2i
D. 3 và 2i
Ta có: (1 - i)z - 1 + 5i = 0 ⇔ (1 - i)z = 1 - 5i
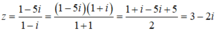
Vậy phần thực và phần ảo của z là 3 và -2
Chọn A
Phần thực và phần ảo của số phức z = ( 1 + 3 i ) 2 là
A. 1 và 3
B. 1 và -3
C. -2 và 2 3
D. 2 và - 2 3
Ta có: z = 1 + 2 3 + 3 i 2 = - 2 + 2 3 i
Vậy phần thực và phần ảo của z là -2 và 2 3
Chọn C
Phần thực và phần ảo của số phức z thỏa mãn z = ( 1 + 2 i ) 2 + ( 1 - 2 i ) 3 là
A. 14 và 6i
B. –14 và 6
C. 14 và – 6
D. –14 và –6
Ta có:
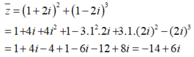
Suy ra z = -14 - 6i. Vậy phần thực và phần ảo của z là: -14 và - 6
Chọn D
Cho phương trình \(z^2+bc+c=0\) có hai nghiệm z1 z2 thỏa mãn z2 - z1 = 4+2i . Gọi A,B là các điểm biểu diễn các nghiệm của phương trình \(z^2-2bz+4c=0\) . Tính độ dài đoạn AB
A: \(8\sqrt{5}\)
B: \(2\sqrt{5}\)
C: \(4\sqrt{5}\)
D: \(\sqrt{5}\)
Cho số phức z = -1 + 3i. Phần thực, phần ảo của z là
A. -1 và 3
B. -1 và -3
C. 1 và -3
D. -1 và -3i
Ta có z = -1 + 3i => z = - 1 - 3 i
Vậy phần thực và phần ảo của z− là -1 và -3.
Chọn đáp án B.