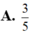
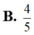
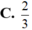
Kí hiệu  z 1 , z 2 là hai nghiệm phức của phương trình  z = 2 + 2 i  Gọi M,N là các điểm biểu diễn của các số phức  z 1 , z 2  Tính  z = 2 + 2 i với O là gốc toạ độ.

A.  T = 2 2 .

B.  T = 2 2

C.  T = 2 2 .

D.  T = 2 2

Kí hiệu z₁, z₂ là hai nghiệm phức của phương trình z 2 + z + 2 = 0  Tính  z 1 z 2 + z 2 z 1

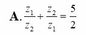
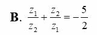
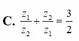
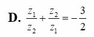
Kí hiệu z₁, z₂ là hai nghiệm phức của phương trình z 2 + z + 2 = 0 .  Tính z 1 z 2 + z 2 z 1

A.  z 1 z 2 + z 2 z 1 = 5 2

B.  z 1 z 2 + z 2 z 1 = - 5 2

C. z 1 z 2 + z 2 z 1 = 3 2

D.  z 1 z 2 + z 2 z 1 = - 3 2

Kí hiệu là hai nghiệm phức của phương trình 3 z 2   -   z   +   1   =   0  .Tính P = z 1   +   z 2  

A .   P   =   14 3

B .   P   =   2 3

C .   P   =   3 3

D .   P   =   2 3 3

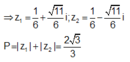
Kí hiệu  z 1 , z 2 là hai nghiệm phức của phương trình 3 z 2 - z + 1 = 0 . Tính  | z 1 | + | z 2 | .

A. 1/3.

B.  3 3

C.  2 3 3

D. 3

Kí hiệu z 1 ,   z 2  là hai nghiệm phức của phương trình 3 z 2 - z + 1 = 0. Tính P = | z 1 |+| z 2 |

A. P =  3 3

B. P = A. P =  3 3

C. P = 2 3

D. P = 14 3

Kí hiệu  z 1 , z 2 là hai nghiệm phức của phương trình z 2 - z + 1 = 0 . Mệnh đề nào dưới đây đúng

A. z 1 = - z 2 .

B.  z 1 = z 2 ¯ . .

C.  z 1 = z 2 .

D.  z 1 = - z 2 ¯

Kí hiệu  z 1 ,   z 2 là hai nghiệm phức của phương trình z 2 + z + 2 2018 = 0 . Tính | z 1 | + | z 2 | .

A.  2 2019

B.  2 1019

C.  2 1010

D.  2 2018

Kí hiệu z 1 , z 2  là hai nghiệm phức của phương trình z 2 + z + 1 = 0  

Giá trị của biểu  thức P= z 1 2 + z 2 2 + z 1 z 2  bằng:

A. P=2

B. P=-1

C. P=0

D. P=1

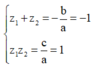
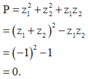
Kí hiệu z 1 ,   z 2  là hai nghiệm phức của phương trình z 2 + z + 1 = 0 . Giá trị của biểu thức P = z 1 2 + z 2 2 + z 1 z 2  bằng:

A. P = - 1 .

B. P = 2 .

C. P = 1 .

D. P = 0 .