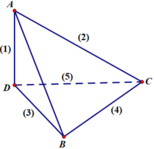
Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (DBC) và D B C ^ = 90 ° . Khi quay các cạnh của tứ diện xung quanh trục là cạnh AB, có bao nhiêu hình nón được tạo thành?
![]()
![]()
![]()
![]()
Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (DBC) và D B C = 90 ° . Khi quay các cạnh của tứ diện xung quanh trục là cạnh AB, có bao nhiêu hình nón được tạo thành?
A. 1
B. 2
C. 3
D. 4
Đáp án C
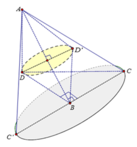
Trong 5 cạch còn lại (không kể cạnh AB) chỉ có 3 cạnh AD, DB, AC khi quay quanh trục AB tạo ra các hình nón. Do đó có 3 hình nón được tạo thành (như hình vẽ).

Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (DBC) và DBC = 900. Khi quay các cạnh của tứ diện xung quanh trục là cạnh AB, có bao nhiêu hình nón được tạo thành?
A. 1
B. 2
C. 3
D.4

Đáp án C
Trong 5 cạch còn lại (không kể cạnh AB) chỉ có 3 cạnh AD, DB, AC khi quay quanh trục AB tạo ra các hình nón. Do đó có 3 hình nón được tạo thành (như hình vẽ).
Chú ý: Do CB ⊥ (ADB) => CB ⊥ AB, do đó CB quay quanh AB chỉ tạo ra hình tròn mà không phải là hình nón.
Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (DBC) và D B C ^ = 90 0 . Khi quay các cạnh của tứ diện xung quanh trục là cạnh AB, có bao nhiêu hình nón được tạo thành?
A. 1.
B. 2.
C. 3.
D. 4.
Đáp án là C
Điều kiện để tạo thành hình nón:
+ Cắt nhau ở đầu mút
+ Góc tạo bởi giữa 2 đường đó phải khác 90 độ
Áp vào hình ta sẽ được
+ AD thỏa mãn
+ AC thỏa mãn
+ DB thỏa mãn
+ BC không thỏa mãn vì BC vuông góc với (ADB) => góc ABC là 90 độ
+ CD không thỏa mãn vì không cắt AB
Vậy có 3 đường thỏa mãn
Cho hình tứ diện ABCD có AD vuông góc với mặt phẳng (ABC), tam giác ABC có A B = 3 a , A C = 4 a , B C = 5 a . Tính góc giữa hai mặt phẳng (ABC) và (DBC), biết khối tứ diện ABCD có thể tích bằng 24 3 a 3 15 .
A. 30°
B. 45°
C. 60°
D. 90°
Đáp án A.
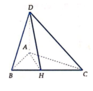
Từ dữ liệu đề bài ta thấy A B 2 + A C 2 = B C 2 ⇒ tam giác ABC vuông tại A.
Trong mặt phẳng A B C kẻ A H ⊥ B C tại H.
Ta có D A ⊥ B C A H ⊥ B C D A ∈ D A H ; A H ∈ D A H D A ∩ A H = A ⇒ D H ⊥ B C (định lý ba đường vuông góc).
Ta có A B C ∩ D B C = B C A H ⊥ B C ; D H ⊥ B C A H ∈ A B C ; D H ∈ D B C ⇒ A B C , D B C ^ = A H D ^ .
Ta có A H = A B . A C B C = 3 a .4 a 5 a = 12 a 5 .
Tam giác ADH vuông tại A.
⇒ tan A H D ^ = D A A H = 3. V A B C D S A B C 12 a 5 = 3.24 3 a 3 15. 1 2 .3 a .4 a 12 a 5 = 3 3
⇒ A H D ^ = 30 °
Vậy ta chọn A.
Cho tứ diện ABCD có (ABC) vuông góc với (DBC), hai tam giác ABC, DBC là tam giác đều cạnh a. Gọi (S) là mặt cầu đi qua B, c và tiếp xúc với đường thẳng AD tại A. Tính bán kính R của mặt cầu (S).
A. R = a 5
B. R = a 6 3
C. R = a 6 5
C. R = a 3
Cho tứ diện ABCD có (ABC) vuông góc với (DBC), hai tam giác ABC, DBC là tam giác đều cạnh a. Gọi (S) là mặt cầu đi qua B, c và tiếp xúc với đường thẳng AD tại A. Tính bán kính R của mặt cầu (S).
![]()
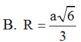
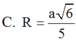
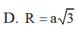
Cho tứ diện ABCD có (ABC) vuông góc với (DBC), hai tam giác ABC, DBC là tam giác đều cạnh a. Gọi (S) là mặt cầu đi qua B, c và tiếp xúc với đường thẳng AD tại A. Tính bán kính R của mặt cầu (S).
A. R = a 6
B. R = a 6 3
C. R = a 6 5
D. R = a 3
Đáp án là B

Gọi K là trọng tâm tam giác ABC, N đỗi xứng với D qua J, qua K kẻ KO song song với DN ta có O là tâm mặt cầu cần xác định.
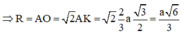
Cho tứ diện ABCD có (ABC) vuông góc với (DBC), hai tam giác ABC, DBC là các tam giác đều cạnh a. Gọi (S) là mặt cầu đi qua B, C và tiêp xúc với đường thẳng AD tại A. Bán kính R của mặt cầu (S) bằng
A. R = a 6
B. R = a 6 3
C. R = a 6 5
D. R = a 3
Cho tứ diện ABCD có (ABC) vuông góc với (DBC), hai tam giác ABC, DBC là các tam giác đều cạnh a. Gọi (S) là mặt cầu đi qua B, C và tiêp xúc với đường thẳng AD tại A. Bán kính R của mặt cầu (S) bằng
![]()
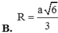
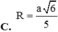
![]()