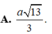
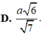
Cho hình chóp S.ABCD có đáy là hình thang vuông ở A và D, cạnh đáy AB = a, cạnh đáy CD = 2a, AD = a. Hình chiếu vuông góc của S lên đáy trùng với trung điểm CD. Biết rằng diện tích mặt bên (SBC) bằng 3 a 2 2 . Thể tích của hình chóp S.ABCD bằng:
A. a 3 B. 3 a 3 2
C. 3 a 3 D. 3 2 a 3
Chọn A.
Gọi H là trung điểm của CD, M là trung điểm của BC. Khi đó HM ⊥ BC, SM ⊥ BC. Dễ thấy tam giác HBC vuông cân ở H, do đó tính được BC, SM. Từ đó tính được SH.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SD= 3 a 2 , hình chiếu vuông góc của S trên mặt phẳng (ABCD) là trung điểm của cạnh AB. Tính theo a thể tích khối chóp S.ABCD
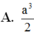
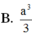
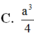
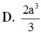
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, hình chiếu vuông góc của S lên mặt phẳng (ABCD) trùng với trung điểm cạnh AD, cạnh SB hợp với đáy một góc 60 ° . Tính theo a thể tích V của khối chóp S.ABCD
A. a 3 15 6
B. a 3 5 4
C. a 3 15 6 3
D. a 3 15 2
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a; hình chiếu vuông góc của S lên mặt phẳng (ABCD) trùng với trung điểm của cạnh AD; cạnh bên SB hợp với đáy một góc 60 o Tính theo a thể tích V của khối chóp S.ABCD.
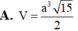
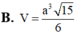
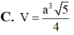
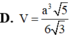
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh hình chiếu vuông góc của S trên mặt phẳng (ABCD) là trung điểm của cạnh AB. Tính theo a thể tích khối chóp S.ABCD
A. a 3 2
B. a 3 3
C. a 3 4
D. 2 a 3 3
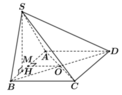
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB vuông tại S và nằm trong mặt phẳng vuông góc với đáy. Thể tích khối cầu ngoại tiếp hình chóp S.ABCD bằng
A. πa 3 3
B. 2 πa 3 3
C. πa 3 6
D. 11 11 πa 3 162
Gọi M là trung điểm AB, do tam giác SAB vuông tại S nên MS = MA = MB
Gọi H là hình chiếu của S trên AB. Từ giả thiết suy ra 
Ta có 
nên là trục của tam giác SAB, suy ra OA = OB = OS (2)
Từ (1) và (2) ta có OS = OA = OB = OC = OD.
Vậy O là tâm mặt cầu ngoại tiếp khối chóp S.ABCD bán kính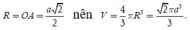 
Chọn B.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Hình chiếu của S trên mặt phẳng (ABCD) trùng với trung điểm của cạnh AB. Cạnh bên S A = 3 a 2 . Tính thể tích khối chóp S.ABCD theo a.
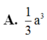
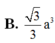
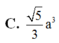
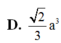
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Hình chiếu của S trên mặt phẳng (ABCD) trùng với trung điểm của cạnh AB. Cạnh bên S D = 3 a 2 . Tính thể tích khối chóp S . A B C D theo a.
A. 1 3 a 3
B. 3 3 a 3
C. 5 3 a 3
D. 2 3 a 3
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Hình chiếu của S trên mặt phẳng (ABCD) trùng với trung điểm của cạnh AB. Cạnh bên SD = 3 a 2 . Tính thể tích khối chóp S.ABCD theo a.
A. 1 3 a 3
B. 3 3 a 3
C. 6 3 a 3
D. 2 3 a 3
Đáp án A
Ta có A D = H A 2 + A D 2 = a 2 2 + a 2 = a 5 2 ⇒ S H = S D 2 - A D 2 = a
Thể tích khối chóp đã cho là: V = 1 3 S H . S A B C D = 1 3 a . a 2 = 1 3 a 3 .
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a 2 . Tam giác SAC vuông cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối cầu ngoại tiếp hình chóp S.ABCD.
A. 2 π a 3 3
B. 4 π a 3 3
C. 2 π a 3 3
D. 4 π a 3
