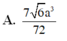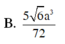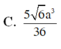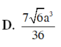Hình chóp tứ giác đều S.ABCD có mấy mặt phẳng đối xứng
A. 1
B. 2
C. 3
D. 4
Những câu hỏi liên quan
Hình chóp tứ giác đều có mấy mặt phẳng đối xứng
A. 1
B. 2
C. 3
D. 4
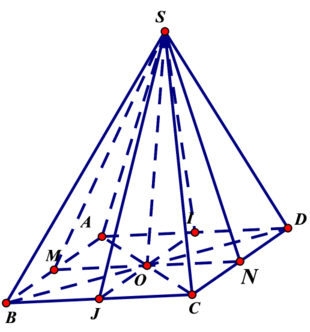
Hình chóp tứ giác đều có 4 mặt phẳng đối xứng đó là:
(SAC), (SBD), (SMN), (SIJ), với M, N, I, J lần lượt là trung điểm của AB, CD, DA, BC.
Chọn D.
Đúng 0
Bình luận (0)
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên hợp với đáy một góc
60
°
. Gọi M là điểm đối xứng với C qua D; N là trung điểm của SC, mặt phẳng ( BMN) chia khối chóp S.ABCD thành hai phân. Tính tỉ số thể tích giữa hai phần đó A.
1
5
B.
7
3
. C.
1
7
D. ...
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên hợp với đáy một góc 60 ° . Gọi M là điểm đối xứng với C qua D; N là trung điểm của SC, mặt phẳng ( BMN) chia khối chóp S.ABCD thành hai phân. Tính tỉ số thể tích giữa hai phần đó
A. 1 5
B. 7 3 .
C. 1 7
D. 7 5
Cho hình chóp tứ giác đều S.ABCD. Gọi N là trung điểm của SB, M là điểm đối xứng với B qua A. Mặt phẳng (MNC) chia khối chóp S.ABCD thành hai phần có thể tích lần lượt là
V
1
,
V
2
với
V
1
V
2
. Tính tỉ số
V
1
V
2
. A....
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD. Gọi N là trung điểm của SB, M là điểm đối xứng với B qua A. Mặt phẳng (MNC) chia khối chóp S.ABCD thành hai phần có thể tích lần lượt là V 1 , V 2 với V 1 < V 2 . Tính tỉ số V 1 V 2 .
A. 5 9
B. 5 11
C. 5 7
D. 5 6
Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên hợp đáy một góc
60
∘
. Gọi M là điểm đối xứng với C qua D, N là trung điểm SC. Mặt phẳng (BMN) chia khối chóp S.ABCD thành hai khối đa diện. Tính thể tích V A.
V
7
6
a
3
36
B.
V...
Đọc tiếp
Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên hợp đáy một góc 60 ∘ . Gọi M là điểm đối xứng với C qua D, N là trung điểm SC. Mặt phẳng (BMN) chia khối chóp S.ABCD thành hai khối đa diện. Tính thể tích V
A. V = 7 6 a 3 36
B. V = 7 6 a 3 72
C. V = 5 6 a 3 72
D. V = 5 6 a 3 36
Đáp án C
Ta có: 2 O D 2 = a 2 ⇒ O D = a 2
⇒ S O = O D tan 60 ∘ = a 2 . 3 = a 3 2
Gọi H là hình chiếu của N lên (ABCD) là trung điểm của OC.
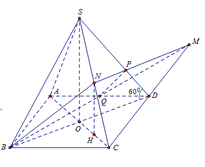
Ta có: N H = S O 2 = a 6 4 ; S M B C = S A B C D = a 2
V N . B C M = 1 3 N H . S M B C = 1 3 . a 6 4 . a 2 = a 3 6 12
Ta có:
M D D C . C S C N . N P P M = 1 ⇔ 1.2. N P P M = 1 ⇔ N P P M = 1 2 ⇒ P M M N = 2 3
Ta có: V M . D P Q V M . B C N = P M M N . M D M C . M Q M B = 2 3 . 1 2 . 1 2 = 1 6
⇒ V N p Q D C A = 5 6 V N . B C M = 5 6 . a 3 6 12 = 5 a 3 6 72
Đúng 0
Bình luận (0)
Cho hình chóp tứ diện đều S.ABCD có canh đáy a, cạnh bên hợp với đáy một góc
60
o
. Gọi M là điểm đối xứng với C qua D, N là trung điểm của SC, mặt phẳng (BMN) chia khối chóp S.ABCD thành 2 phần. Tính tỉ số thể tích của hai phần đó. A.
7
5
B.
7
3
C.
1
7
D.
1...
Đọc tiếp
Cho hình chóp tứ diện đều S.ABCD có canh đáy a, cạnh bên hợp với đáy một góc 60 o . Gọi M là điểm đối xứng với C qua D, N là trung điểm của SC, mặt phẳng (BMN) chia khối chóp S.ABCD thành 2 phần. Tính tỉ số thể tích của hai phần đó.
A. 7 5
B. 7 3
C. 1 7
D. 1 5
Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt phẳng đáy bằng
60
°
Gọi M là điểm đối xứng vưới C qua D và N là trung điểm của cạnh SC. Mặt phẳng (BMN) chia khối chóp S.ABCD thành hai khối đa diện
H
1
và
H
2
trong đó
H
1
chứa điểm C. Thể tích của khối là A. ...
Đọc tiếp
Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt phẳng đáy bằng 60 ° Gọi M là điểm đối xứng vưới C qua D và N là trung điểm của cạnh SC. Mặt phẳng (BMN) chia khối chóp S.ABCD thành hai khối đa diện H 1 và H 2 trong đó H 1 chứa điểm C. Thể tích của khối là
A. 7 6 a 3 72
B. 5 6 a 3 72
C. 5 6 a 3 36
D. 7 6 a 3 36
Đáp án B
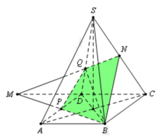
Nối MN cắt SD tại Q, MB cắt AD tại P
Suy ra mp(BMN) cắt khối chóp S.ABCD theo thiết diện tứ giác BPQN và chia khối chóp thành 2 đa diện
Đúng 0
Bình luận (0)
Cho khối chóp tứ giác đều S.ABCD có dạng đáy bằng a, góc giữa cạnh bên và mặt phẳng đáy bằng
60
0
. Gọi M là điểm đối xứng với C qua D và N là trung điểm của cạnh SC. Mặt phẳng (BMN) chia khối chóp S.ABCD thành hai khối đa diện (
H
1
) và (
H
2
), trong đó (
H
1
) chứa điểm C. Thể tích của khối (
H...
Đọc tiếp
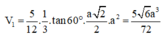
Cho khối chóp tứ giác đều S.ABCD có dạng đáy bằng a, góc giữa cạnh bên và mặt phẳng đáy bằng 60 0 . Gọi M là điểm đối xứng với C qua D và N là trung điểm của cạnh SC. Mặt phẳng (BMN) chia khối chóp S.ABCD thành hai khối đa diện ( H 1 ) và ( H 2 ), trong đó ( H 1 ) chứa điểm C. Thể tích của khối ( H 1 ) là:
Cho khối chóp tứ giác đều S.ABCD có dạng đáy bằng a, góc giữa cạnh bên và mặt phẳng đáy bằng
60
°
. Gọi M là điểm đối xứng với C qua D và N là trung điểm của cạnh SC. Mặt phẳng (BMN) chia khối chóp S.ABCD thành hai khối đa diện
H
1
và
H
2
, trong đó
H
1
chứa điểm C. Thể t...
Đọc tiếp
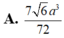
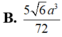
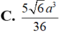
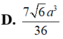
Cho khối chóp tứ giác đều S.ABCD có dạng đáy bằng a, góc giữa cạnh bên và mặt phẳng đáy bằng 60 ° . Gọi M là điểm đối xứng với C qua D và N là trung điểm của cạnh SC. Mặt phẳng (BMN) chia khối chóp S.ABCD thành hai khối đa diện H 1 và H 2 , trong đó H 1 chứa điểm C. Thể tích của khối H 1 là:
A. 7 6 a 3 72
B. 5 6 a 3 72
C. 5 6 a 3 36
D. 7 6 a 3 36
Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt phẳng đáy bằng
60
0
. Gọi M là điểm đối xứng vưới C qua D và N là trung điểm của cạnh SC. Mặt phẳng (BMN) chia khối chóp S.ABCD thành hai khối đa diện
(
H
1
)
và
(
H
2
)
trong đó
(
H
1
)
chứa điểm C. Thể tích...
Đọc tiếp
Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt phẳng đáy bằng 60 0 . Gọi M là điểm đối xứng vưới C qua D và N là trung điểm của cạnh SC. Mặt phẳng (BMN) chia khối chóp S.ABCD thành hai khối đa diện ( H 1 ) và ( H 2 ) trong đó ( H 1 ) chứa điểm C. Thể tích của khối ( H 1 ) là
