Hình ABCD có số góc vuông là:
A. 2
B. 3
C. 4
Có hình chóp S. ABCD có đáy là hình vuôn cạnh a . SA vuông góc (ABCD) và SA= a căn6/3
a. Chứng minh CD vuông góc (SAD)
b. P, Q lần lượt là hình chiếu vuông góc của A lên SB , SD . chứng minh PQ vuông góc SC
C. Tính góc SC và (ABCD)
Hình chóp SABCD có ABCD là hình vuông SA vuông góc ABCD SA = a√6/3
a,Cm BD vuông góc SC
b, cm SAB vuông góc SBC
c, góc giữa sc và abcd
d, khoảng cách từ a đến scd
1. Cho hình thang ABCD có góc A = góc D = 90 độ , đáy nhỏ AB = a , cạnh bên BC = 2 a . Gọi M , N lần lượt là trung điểm AD , AB
a / Tính số đo các góc ABC , BAN
b/ Chứng minh tam giác NAD đều
c/ Tính MN theo a
2. a/ Tính các góc A , góc B của hình thang ABCD ( AB // CD ) biết góc C = 70 độ , góc D = 40 độ
b/ Cho hình thang ABCD có AB // CD và góc A = góc D . Chứng minh rằng ABCD là hình thang vuông cà AC^2 + BD^2 = AB^2 + CD^2 + 2AD^2
3. Cho tứ giác ABCD :
a/ Chứng minh rằng AB + CD < AC + BD
b/ Cho biết AB + BD < hoặc = AC + CD
Chứng minh rằng AB < AC
4. Cho hình thang ABCD có AC vuông góc BD . CHứng minh rằng :
a/ AB^2 + CD^2 = AD^2 + BC^2
b/ ( AB + CD )^2 = AC^2 + BD^2
bạn hỏi thế này thì chả ai muốn làm -_- dài quá
Bạn gửi từng câu nhò thì các bạn khác dễ làm hơn!
dài quà làm sao mà có thòi gian mà trả lời .bạn hỏi ít thoi chứ
BÀI 1
Cho hình thang vuông ABCD, góc A=góc D=90độ.
a) tìm điểm Ithuộc AD sao cho IC=IB
b)Với điểm I vừa tìm được, giả sử tam giác IBC vuông cân ở I, chứng minh rằng AB+CD=AD
c) Với điểm I vừa tìm được, giả sử DC=1/2 IC,hãy tính góc Bvà C của hình thang ABCD
BÀI 2
Cho tứ giác ABCD, có phân giác góc A cắt CD tại I, biết IC=BC và DC=AD+BC. Chứng minh:
a) ABCD là hình thang
b) BI là phân giác góc ABC
BÀI 3
Cho hình thang ABCD có AB//CD có góc B-góc C=24 độ, góc A=3/2góc B. Tính các góc còn lại
BÀI 4 :
Cho tam giác vuông can A, trên nửa mặt phẳng bờ là BC không chứa A vẽ BD vuông góc BC và BD=BC. Chứng minh :
a) Tứ giác ABCD là hình gì?
b) Tính CD, biết AB=5
MONG MỌI NGƯỜI GIÚP ĐỠ Ạ! MÌNH CẢM ƠN :))
cho hình chóp S.ABCD có ABCD là hình vuông cạnh a, SA vuông góc (ABCD), SA=a căn 2
1.chứng minh : các mặt bên của hình chóp là tam giác vuông
2. (SAC) vuông góc (SBD)
3.Tính (SC,(SAB))
4.tan ((SBD),(ABCD))
5.d(A,(SBC)),d(A,(SCD))
6.d(SC,BD)
7.Hãy chỉ ra điểm I cách đều S,A,B,C,D. tính SI
1.SA \(\perp\)AB , SA\(\perp\)AD =>SAB vuông tại A, SAD vuông tại A
\(\begin{cases}AB\perp BC\left(hvABCD\right)\\SA\perp BC\left(SA\perp mpABCD\right)\end{cases}\) =>(SAB)\(\perp\)BC =>SB\(\perp\)BC =>SBC vuông tại B
\(\begin{cases}AD\perp CD\\SA\perp CD\end{cases}\) =>(SAD)\(\perp\)CD =>SD\(\perp\)CD =>SCD vuông tại D
1. Cho hình vuông ABCD có độ dài cạnh là 6cm. Trên cạnh AB lấy điểm E sao cho diện tích hình vuông ABCD gấp 3 lần diện tích tam giác ADE. Tính AE.
2. Tính số đo các góc của hình bình hành ABCD. Biết A+B+C=230
Cho hình chóp A.ABCD có SA vuông góc (ABCD) , \(SA=a\sqrt{3}\). ABCD là hình vuông cạnh a
Tính góc giữa
a) (SBC) và (SCD)
b) (SAB) và (SBC)
c) (SAD) và (SCD)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a; SA=SB=SC=SD=a√2; O là tâm của hình vuông ABCD.
a) C/m (SAC) và (SBD) cùng vuông góc với (ABCD).
b) C/m (SAC) ⊥(SBD)
c) Tính khoảg cách từ S đến (ABCD)
d) Tính góc giữa đường SB và (ABCD).
e) Gọi M là trung điểm của CD, hạ OH⊥SM, chứng minh H là trực tâm tam giác SCD
f) Tính góc giưa hai mặt phẳng (SCD) và (ABCD)
g) Tính khoảng cách giữa SM và BC; SM và AB.
a: SO vuông góc (ABCD)
=>(SAC) vuông góc (ABCD)
SO vuông góc (ABCD)
=>(SBD) vuông góc (ABCD)
b: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
d: (SB;(ABCD))=(BS;BO)=góc SBO
cos SBO=OB/SB=a*căn 2/2/(a*căn 2)=1/2
=>góc SBO=60 độ
cho hình chóp S ABCD có đáy ABCD là hình chữ nhật. Biết AB= a căn 2; AD= a căn 3; SA vuông góc (ABCD), biết SC = a căn 7
a, tính góc giữa SB và (ABCD)
b. tính góc giữa SC và (SAD)
c, tính góc giữa (SBC) và (ABCD)
d, tính góc giữa (SBD) và (ABCD)
a: (SB;(ABCD))=(BS;BA)=góc SBA
AC=căn a^2+3a^2=2a
SA=căn SC^2-AC^2=a*căn 3
tan SBA=SA/AB=căn 3
=>góc SBA=60 độ
b: (SC;(SAD))=(SC;SD)=góc SCD
SD=căn SA^2+AD^2=2a*căn 3
cos SCD=(CS^2+CD^2-SD^2)/(2*CS*CD)=-2/căn 7
=>góc SCD=139 độ
Đúng ghi Đ, sai ghi S :
Trong hình bên :
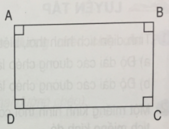
a) AB và DC là hai cạnh đối điện song song với nhau.
b) AB vuông góc với AD.
c) Hình tứ giác ABCD có 4 góc vuông.
d) Hình tứ giác ABCD có 4 cạnh bằng nhau.
a/đ b/đ c/đ d/s