Giải các phương trình sau: (Tìm ĐKXĐ)
a)
b)
Giải các phương trình sau: (Tìm ĐKXĐ)
a)
b)
a.
ĐKXĐ: \(x\ge-1\)
\(\sqrt{x+1}+\sqrt{2x+3}=5\)
\(\Leftrightarrow\sqrt{x+1}-2+\sqrt{2x+3}-3=0\)
\(\Leftrightarrow\dfrac{x-3}{\sqrt{x+1}+2}+\dfrac{2\left(x-3\right)}{\sqrt{2x+3}+3}=0\)
\(\Leftrightarrow\left(x-3\right)\left(\dfrac{1}{\sqrt{x+1}+2}+\dfrac{2}{\sqrt{2x+3}+3}\right)=0\)
\(\Leftrightarrow x-3=0\) (do \(\dfrac{1}{\sqrt{x+1}+2}+\dfrac{2}{\sqrt{2x+3}+3}>0\))
\(\Leftrightarrow x=3\)
b.
Dạng câu này có cách làm riêng, ko tìm ĐKXĐ:
\(\sqrt{3x^2+4x+1}=x-1\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-1\ge0\\3x^2+4x+1=\left(x-1\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge1\\2x^2+6x=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge1\\\left[{}\begin{matrix}x=0\left(ktm\right)\\x=-3\left(ktm\right)\end{matrix}\right.\end{matrix}\right.\)
Vậy pt đã cho vô nghiệm
\(a,ĐK:x\ge-\dfrac{3}{2}\\ PT\Leftrightarrow\sqrt{x+1}-2+\sqrt{2x+3}-3=0\\ \Leftrightarrow\dfrac{x-3}{\sqrt{x+1}+2}+\dfrac{2\left(x-3\right)}{\sqrt{2x+3}+3}=0\\ \Leftrightarrow\left(x-3\right)\left(\dfrac{1}{\sqrt{x+1}+2}+\dfrac{2}{\sqrt{2x+3}+3}\right)=0\)
Dễ thấy ngoặc lớn luôn >0
Do đó \(x-3=0\Leftrightarrow x=3\)
\(b,ĐK:x\le-1\\ PT\Leftrightarrow\sqrt{3x^2+4x+1}=x-1\\ \Leftrightarrow3x^2+4x+1=x^2-2x+1\\ \Leftrightarrow2x^2+6x=0\\ \Leftrightarrow2x\left(x+3\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\left(ktm\right)\\x=-3\left(tm\right)\end{matrix}\right.\)
Giải các phương trình sau:(thêm ĐKXĐ) a)/x-5/=2x+3 b)/x+3/=3x-1c) 3-2x=4
\(\left|x-5\right|=2x+3\) `(1)`
Nếu `x-5>=0<=>x>=5` thì phương trình `(1)` trở thành :
`x-5=2x+3`
`<=>x-2x=3+5`
`<=> -x=8`
`<=>x=-8` ( không thỏa mãn )
Nếu `x-5<0<=>x<5` thì phương trình `(1)` trở thành :
`-(x-5)=2x+3`
`<=> -x+5=2x+3`
`<=>-x-2x=3-5`
`<=> -3x=-2`
`<=>x=2/3` ( thỏa mãn )
Vậy pt đã cho có nghiệm `x=2/3`
__
\(\left|x+3\right|=3x-1\) `(1)`
Nếu `x+3>=0<=>x>=-3` vậy phương trình `(1)` trở thành :
`x+3=3x-1`
`<=> x-3x=-1-3`
`<=> -2x=-4`
`<=>x=2` ( thỏa mãn )
Nếu `x+3<0<=>x<-3` thì phương trình `(1)` trở thành :
`-(x+3)=3x-1`
`<=>-x-3=3x-1`
`<=>-x-3x=-1+3`
`<=>-4x=2`
`<=>x=-1/2` ( không thỏa mãn )
Vậy pt đã cho có nghiệm `x=2`
__
`3-2x=4`
`<=> -2x=4-3`
`<=>-2x=1`
`<=>x=-1/2`
Vậy pt đã cho có nghiệm `x=-1/2`
1,Tìm đkxđ biểu thức \(\sqrt{3-2x}\)
2,giải phương trình :
a,\(\sqrt{3x-1}\)=2
b,\(\sqrt{x-2}\)+ \(\sqrt{4x-8}\)=6
Bài 1:
ĐKXĐ: $3-2x\geq 0\Leftrightarrow x\leq \frac{3}{2}$
Bài 2:
a. ĐKXĐ: $x\geq \frac{1}{3}$
PT $\Leftrightarrow 3x-1=2^2=4$
$\Leftrightarrow x=\frac{5}{3}$ (tm)
b. ĐKXĐ: $x\geq 2$
PT $\Leftrightarrow \sqrt{x-2}+2\sqrt{x-2}=6$
$\Leftrightarrow 3\sqrt{x-2}=6$
$\Leftrightarrow \sqrt{x-2}=2$
$\Leftrightarrow x-2=4$
$\Leftrightarrow x=6$ (tm)
Tìm sai lầm trong các "lời giải" sau:
a) Giải bất phương trình -2x > 23. Ta có:
-2x > 23 ⇔ x > 23 + 2 ⇔ x > 25.
Vậy nghiệm của bất phương trình là x > 25.
b) Giải bất phương trình 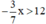 . Ta có:
. Ta có:
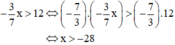
a) Sai lầm là coi -2 là hạng từ và chuyển vế hạng tử này trong khi -2 là một nhân tử.
Lời giải đúng:
-2x > 23
⇔ x < 23 : (-2) (chia cho số âm nên đổi chiều)
⇔ x < -11,5
Vậy nghiệm của bất phương trình là x < -11,5
b) Sai lầm là nhân hai vế của bất phương trình với 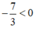 mà không đổi chiều bất phương trình.
mà không đổi chiều bất phương trình.
Lời giải đúng:
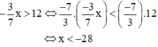
Vậy nghiệm của bất phương trình là x < -28
3.15 giải các phương trình sau :
a) ( x - 6 ) ( 2x - 5 ) ( 3x + 9 ) = 0
b) 2x( x - 3 ) + 5( x - 3 ) = 0
c) ( x^2 - 4 ) - ( x - 2 ) ( 3 - 2x ) =0
3.16 tìm m để phương trình sau có nghiệm :
x=-7 ( 2m - 5 )x - 2m^2 + 8
3.17 giải các phương trình sau :
a) ( 2x - 1 )^2 - ( 2x + 1 ) = 0
\(a,\left(x-6\right)\left(2x-5\right)\left(3x+9\right)=0\Leftrightarrow\left[{}\begin{matrix}x-6=0\Leftrightarrow x=6\\2x-5=0\Leftrightarrow x=\dfrac{5}{2}\\3x+9=0\Leftrightarrow x=-3\end{matrix}\right.\)
\(b,2x\left(x-3\right)+5\left(x-3\right)=0\Leftrightarrow\left(2x+5\right)\left(x-3\right)=0\Leftrightarrow\left[{}\begin{matrix}x-3=0\Leftrightarrow x=3\\2x+5=0\Leftrightarrow x=-\dfrac{5}{2}\end{matrix}\right.\)
\(c,x^2-4-\left(x-2\right)\left(3-2x\right)=0\Leftrightarrow\left(x-2\right)\left(x+2\right)-\left(x-2\right)\left(3-2x\right)=0\Leftrightarrow\left(x-2\right)\left(x+2-3+2x\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{1}{3}\end{matrix}\right.\)
\(x=-7\left(2m-5\right)x-2m^2+8\Leftrightarrow x+7\left(2m-5\right)=8-2m^2\Leftrightarrow x\left(14m-34\right)=8-2m^2\)
\(ycđb\Leftrightarrow14m-34\ne0\Leftrightarrow m\ne\dfrac{34}{14}\)\(\Rightarrow x=\dfrac{8-2m^2}{14m-34}\)
\(3.17\Leftrightarrow4x^2-4x+1-2x-1=0\Leftrightarrow4x^2-6x=0\Leftrightarrow x\left(4x-6\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{3}{2}\end{matrix}\right.\)
3.15:
a, \(\Leftrightarrow\left\{{}\begin{matrix}x-6=0\\2x-5=0\\3x+9=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=6\\x=\dfrac{5}{2}\\x=-\dfrac{9}{3}=-3\end{matrix}\right.\)
b, \(\Leftrightarrow\left(x-3\right)\left(2x+5\right)=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-3=0\\2x+5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\x=-\dfrac{5}{2}\end{matrix}\right.\)
c, \(\Leftrightarrow\left(x-2\right)\left(x+2\right)-\left(x-2\right)\left(3-2x\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+2-3+2x\right)=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-2=0\\3x-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\x=\dfrac{1}{3}\end{matrix}\right.\)
3.16
\(\Leftrightarrow\left(2m-5\right).-7-2m^2+8=0\)
\(\Leftrightarrow-14m+35-2m^2+8=0\)
\(\Leftrightarrow-14m-2m^2+43=0\)
\(\Leftrightarrow-2\left(7m+m^2\right)=-43\)
\(\Leftrightarrow m\left(7-m\right)=\dfrac{43}{2}\)
\(\Leftrightarrow\dfrac{m\left(7-m\right)}{1}-\dfrac{43}{2}=0\)
\(\Leftrightarrow\dfrac{14m-2m^2}{2}-\dfrac{43}{2}=0\)
pt vô nghiệm
\(\frac{3x}{2x-4}-\frac{x+2}{x+2}=\frac{-2x^2}{2x^2-8}\)
giải phương trình, tìm đkxđ.
Cho bt A=\(\left(\frac{1}{\sqrt{x-1}}+\frac{1}{\sqrt{x+1}}\right)^2.\frac{^{x^2}-1}{2}-\sqrt{1-x^2}\)
a) Tìm ĐKXĐ
b)Rút gọn
c) giải phương trình theo x khi A=-2
giải các hệ phương trình
\(\left\{{}\begin{matrix}\dfrac{2x+1}{4}-\dfrac{y-2}{3}=\dfrac{1}{12}\\\dfrac{x+5}{2}=\dfrac{y+7}{3}-4\end{matrix}\right.\)
b2.
\(A=\sqrt{3+\sqrt{5}}+\sqrt{7-3\sqrt{5}}-\sqrt{2}\)
B3. Tìm ĐKXĐ
\(\dfrac{1}{x\sqrt{x}+1}-\dfrac{2}{\sqrt{x}+1}\)
b4. so sánh A với 1
A=\(\dfrac{\sqrt{x}}{x-\sqrt{x}+1}\)
b5.tính
a,\(\sin47+2\sin38-\cos43-\cos52\)
b, \(C=\dfrac{2\sin^2x-1}{\sin x-\cos x}\)
Bài 2:
Ta có: \(A=\sqrt{3+\sqrt{5}}+\sqrt{7-3\sqrt{5}}-\sqrt{2}\)
\(=\dfrac{\sqrt{6+2\sqrt{5}}+\sqrt{14-6\sqrt{5}}-2}{\sqrt{2}}\)
\(=\dfrac{\sqrt{5}+1+3-\sqrt{5}-2}{\sqrt{2}}=\sqrt{2}\)
Em hãy chọn khẳng định đúng trong hai khẳng định dưới đây :
a) Hai phương trình tương đương với nhau thì phải có cùng ĐKXĐ
b) Hai phương trình có cùng ĐKXĐ có thể không tương đương với nhau