Cho hai biểu thức A = 7 x + 8 và B = x x - 3 + 2 x - 24 x - 9 với x ≥ 0, x ≠ 9. Tính giá trị của biểu thức A khi x = 25
A. 7 13
B. 7
C. 7 33
D. 13 7
Bài 1: Cho hai biểu thức \(A=\dfrac{7}{\sqrt{x}+8}\)và \(B=\dfrac{\sqrt{x}}{\sqrt{x}-3}+\dfrac{2\sqrt{x}-24}{x-9}\) với x\(>\)0 và x\(\ne\)0
a, Tính giá trị của A khi x=25
b, CM: \(B=\dfrac{\sqrt{x}+8}{\sqrt{x}+3}\)
c, Tìm x để biểu thức P= A\(\times\)B có giá trị nguyên
a: Khi x=25 thì \(A=\dfrac{7}{5+8}=\dfrac{7}{13}\)
b: \(B=\dfrac{\sqrt{x}\left(\sqrt{x}+3\right)+2\sqrt{x}-24}{x-9}\)
\(=\dfrac{x+5\sqrt{x}-24}{x-9}=\dfrac{\left(\sqrt{x}+8\right)\left(\sqrt{x}-3\right)}{x-9}=\dfrac{\sqrt{x}+8}{\sqrt{x}+3}\)
c: P=A*B
\(=\dfrac{\sqrt{x}+8}{\sqrt{x}+3}\cdot\dfrac{7}{\sqrt{x}+8}=\dfrac{7}{\sqrt{x}+3}\)
P là số nguyên
=>căn x+3 thuộc Ư(7)
=>căn x+3=7
=>x=16
Cho hai biểu thức: A = 1 + 1 2 + x và B = 12 x 3 + 8 . Tìm x sao cho A = B.
A. x = 0
B. x =1
C. x = -1
D. Cả A và B
Cho hai biểu thức: A = 1 - 1 2 - x và B = 12 x 3 - 8 . Giá trị của x để A = B là
A. x = 0
B. x = 1
C. Không có x
D. x = 2
Cho hai biểu thức A=\(\dfrac{x+7}{\sqrt{x}}\) và B=\(\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{2\sqrt{x}-1}{\sqrt{x}-3}-\dfrac{2x-\sqrt{x}-3}{x-9}\)(x>0,x≠9)
a.tính giá trị biểu thức A khi x=121
b.rút gọn biểu thức B
c.đặt S=1/B+A.So sánh S và \(|s|\)
a: Thay x=121 vào A, ta được:
\(A=\dfrac{121+7}{\sqrt{121}}=\dfrac{128}{11}\)
b: \(B=\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{2\sqrt{x}-1}{\sqrt{x}-3}-\dfrac{2x-\sqrt{x}-3}{x-9}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{2\sqrt{x}-1}{\sqrt{x}-3}-\dfrac{2x-\sqrt{x}-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)+\left(2\sqrt{x}-1\right)\left(\sqrt{x}+3\right)-2x+\sqrt{x}+3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{x-3\sqrt{x}+2x+6\sqrt{x}-\sqrt{x}-3-2x+\sqrt{x}+3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{x-3\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{\sqrt{x}}{\sqrt{x}+3}\)
c: \(S=\dfrac{1}{B}+A=\dfrac{\sqrt{x}+3}{\sqrt{x}}+\dfrac{x+7}{\sqrt{x}}=\dfrac{x+\sqrt{x}+10}{\sqrt{x}}\)
Vì \(x+\sqrt{x}+10=\sqrt{x}\left(\sqrt{x}+1\right)+10>=10>0\forall x\) thỏa mãn ĐKXĐ
và \(\sqrt{x}>0\forall\)x thỏa mãn ĐKXĐ
nên S>0 với mọi x thỏa mãn ĐKXĐ
=>S=|S|
Tính rồi so sánh giá trị của hai biểu thức (theo mẫu).
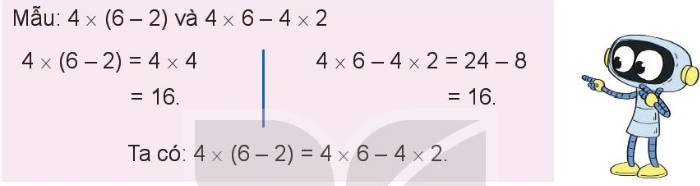
a) 23 x (7 - 4) và 23 x 7 - 23 x 4
b) (8 - 3) x 9 và 8 x 9 - 3 x 9
a,
23 x (7 - 4) = 23 x 3 = 69
23 x 7 - 23 x 4 = 161 - 92 = 69
Ta có: 23 x (7 - 4) = 23 x 7 - 23 x 4
b,
(8 - 3) x 9 = 5 x 9 = 45
8 x 9 - 3 x 9 = 72 - 27 = 45
Ta có: (8 - 3) x 9 = 8 x 9 - 3 x 9
Cho 2 biểu thức A= \(\dfrac{7}{\sqrt{x}+8}\) và B=\(\dfrac{\sqrt{x}}{\sqrt{x}-3}+\dfrac{2\sqrt{x}-24}{x-9}\)
a) Chứng minh B= \(\dfrac{\sqrt{x}+8}{\sqrt{x}+3}\)
b) Tìm GTLN của B
c) Tìm số nguyên x để biểu thức P = A.B có giá trị là số nguyên.
Help
Cho hai biểu thức \(A=\dfrac{7}{\sqrt{x+8}}\)và \(B=\dfrac{\sqrt{x}}{\sqrt{x-3}}+\dfrac{2\sqrt{x-24}}{x-9}\)với x > 0 ; x khác 9
Tính giá trị của A khi x = 16
Cho hai biểu thức: P = 268 + 57 x m - 1659:n và
Q = (1085 - 35 x n):m + 4 x h.
So sánh giá trị của 2 biểu thức P và Q biết m = 8, n = 7, h = 58
Với m=8,n=7,h=58 thì:
P=268+57×m−1659:n
=268+57×8−1659:7
=268+456−237
=724−237
=487
Q=(1085−35×n):m+4×h
=(1085−35×7):8+4×58
=(1085−245):8+232
=840:8+232
=105+232
=337
Mà 487>337 nên P>Q.
Vậy với m=8,n=7,h=58 thì P>Q.
Chú ý
Học sinh cần nhớ thứ tự thực hiện phép tính, từ đó tính đúng giá trị của P và Q .
Cho hai biểu thức:
A = \(\dfrac{x-7}{\sqrt{x}}\) và B = \(\dfrac{\sqrt{x}}{\sqrt{x}+2}\) với \(x\ge0;x\ne4\)
Tìm tất cả các giá trị nguyên của x để biểu thức P = A.B có giá trị nguyên
P = A.B = \(\dfrac{x-7}{\sqrt{x}+2}=\dfrac{\left(x-4\right)-3}{\sqrt{x}+2}=\dfrac{\left(\sqrt{x}-2\right).\left(\sqrt{x}+2\right)-3}{\sqrt{x}+2}\)
\(=\sqrt{x}-2-\dfrac{3}{\sqrt{x}+2}\)
\(P\inℤ\) <=> x là số chính phương và \(\dfrac{3}{\sqrt{x}+2}\inℤ\)
mà \(\sqrt{x}+2\ge2\Rightarrow\dfrac{3}{\sqrt{x}+2}\inℤ\Leftrightarrow\sqrt{x}+2=3\)
\(\Leftrightarrow x=1\) (thỏa)
Vậy x = 1 thì P \(\inℤ\)
Tìm các giá trị nguyên của n để hai biểu thức A và B đồng thời chia hết cho biểu thức C: a, A= x^3.y^3n-1, B=x^3n.y^7-2n và C= 6x^n.y^4
b, A=x^2n.y^6-3n.z^2, B=x^3.y^3-2n
C=x^3.y^4