Mặt cầu có tâm O và tiếp xúc với mặt phẳng (P): x+2y-2z-6=0 có phương trình là
A. x 2 + y 2 + z 2 = 16 .
B. x 2 + y 2 + z 2 = 9 .
C. x 2 + y 2 + z 2 = 6 .
D. x 2 + y 2 + z 2 = 4
Một quả cầu (S) có tâm I(-1;2;1) và tiếp xúc với mặt phẳng (P): x-2y-2z-2=0 có phương trình là:
A. ( S ) : x + 1 2 + y - 2 2 + z - 1 2 = 3
B. ( S ) : x + 1 2 + y - 2 2 + z + 1 2 = 3
C. ( S ) : x + 1 2 + y - 2 2 + z + 1 2 = 9
D. ( S ) : x + 1 2 + y - 2 2 + z - 1 2 = 9
Đáp án D
Phương pháp
+) (S) tiếp xúc với (P) nên d(I;(P))=R
+) Phương trình mặt cầu tâm I(a;b;c) bán kính R là
![]()
Cách giải
Ta có
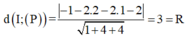
Vậy phương trình mặt cầu là: ( S ) : x + 1 2 + y - 2 2 + z - 1 2 = 9
Trong không gian với hệ tọa độ Oxyz, mặt cầu (S) có tâm I(-1;2;1) và tiếp xúc với mặt phẳng (P): x-2y-2z-2=0 có phương trình là
![]()
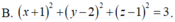
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, cho điểm I(1;0;-2) và mặt phẳng (P) có phương trình x + 2y -2z +4 =0. Phương trình mặt cầu (S) tâm I và tiếp xúc với mặt phẳng (P) là:
A. (x-1)² + y² + (z+2)² =9
B. (x-1)² +y² + (z+2)² =3
C. (x+1)² + y² + (z-2)² =3
D. (x+1)² + y² + (z-2)² =9.
Đáp án A
Do (P) tiếp xúc với (S) nên bán kính của (S) là R = d(I, (P)) = 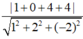 = 3. Vậy phương trình mặt cầu (S) là (x-1)² + y² + (z+2)² =9.
= 3. Vậy phương trình mặt cầu (S) là (x-1)² + y² + (z+2)² =9.
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x = t y = − 1 z = − t và 2 mặt phẳng (P),(Q) lần lượt có phương trình x + 2 y + 2 z + 3 = 0 ; x + 2 y + 2 z + 7 = 0 . Viết phương trình mặt cầu (S) có tâm I thuộc đường thẳng d, tiếp xúc với hai mặt phẳng (P) và (Q).
A. x + 3 2 + y + 1 2 + z − 3 2 = 4 9
B. x − 3 2 + y + 1 2 + z + 3 2 = 4 9
C. x + 3 2 + y + 1 2 + z + 3 2 = 4 9
D. x − 3 2 + y − 1 2 + z + 3 2 = 4 9
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x = t y = - 1 z = - t và 2 mặt phẳng P , Q lần lượt có phương trình x + 2 y + 2 z + 3 = 0 ; x + 2 y + 2 z + 7 = 0 . Viết phương trình mặt cầu (S) có tâm I thuộc đường thẳng d, tiếp xúc với hai mặt phẳng P và Q .
A. x + 3 2 + y + 1 2 + z - 3 2 = 4 9
B. x - 3 2 + y + 1 2 + z - 3 2 = 4 9
C. x + 3 2 + y + 1 2 + z + 3 2 = 4 9
D. x - 3 2 + y - 1 2 + z + 3 2 = 4 9
Trong không gian Oxyz, mặt cầu có tâm I(1;2;−1) và tiếp xúc với mặt phẳng (P): x-2y-2z-8=0 có phương trình là
![]()
![]()
![]()
![]()
Viết phương trình mặt cầu (S) có tâm I thuộc đường thẳng ∆ : x = t y = - 1 z = - t và (S) tiếp xúc với hai mặt phẳng ( P ) : x + 2 y + 2 z + 3 = 0 v à ( Q ) : x + 2 y + 2 z + 7 = 0 .
A. x - 3 2 + y + 1 2 + z + 3 2 = 4 9
B. x + 3 2 + y + 1 2 + z - 3 2 = 4 9
C. x + 3 2 + y - 1 2 + z - 3 2 = 4 9
D. x - 3 2 + y - 1 2 + z + 3 2 = 4 9
Chọn A.
Gọi I(t;-1;-t) ∈ Δ là tâm mặt cầu (S) cần tìm.
Theo giả thiết mặt cầu tiếp xúc với hai mặt phẳng (P) và (Q) nên:
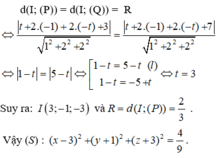
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x 2 = y - 3 1 = z - 2 1 và hai mặt phẳng
(P): x-2y+2z=0. (Q): x-2y+3z-5=0. Mặt cầu (S) có tâm I là giao điểm của đường thẳng d và mặt phẳng (P). Mặt phẳng (Q) tiếp xúc với mặt cầu (S). Viết phương trình của mặt cầu (S).
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x 2 = y - 3 1 = z - 2 1 và hai mặt phẳng
P x - 2 y + 2 z = 0 ; Q : x - 2 y + 3 z - 5 = 0 . Mặt cầu (S) có tâm I là giao điểm của đường thẳng d và mặt phẳng (P). Mặt phẳng (Q) tiếp xúc với mặt cầu (S). Viết phương trình của mặt cầu (S).
A. S : x + 2 2 + y + 4 2 + z + 3 2 = 1
B. S : x - 2 2 + y - 4 2 + z - 3 2 = 6
C. S : x - 2 2 + y - 4 2 + z - 3 2 = 2 7
D. S : x - 2 2 + y + 4 2 + z + 4 2 = 8
Chọn C.
Phương pháp: Lần lượt tìm các yếu tố tâm và bán kính của mặt cầu.
Cách giải: Tọa độ tâm mặt cầu thỏa mãn hệ
