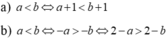Cho a < b, hãy so sánh: a – 2 và b – 2

Những câu hỏi liên quan
Cho a < b, hãy so sánh:
a) a + 1 và b + 1; b) 2 - a và 2 - b
. Cho a<b , hãy so sánh :
a/ a + 2 và b +2
b/ 3a – 2 và 3b +2 .
`a)a<b<=>a+2<b+2`
`b)a<b<=>3a<3b<=>3a-2<3b-2<3b+2`
Đúng 0
Bình luận (1)
Cho a > b > 0. Hãy so sánh \(\sqrt{a+2}-\sqrt{a}\) và \(\sqrt{b+2}-\sqrt{b}\)
\(\sqrt{a+2}-\sqrt{a}=\dfrac{2}{\sqrt{a+2}+\sqrt{a}}\)
\(\sqrt{b+2}-\sqrt{b}=\dfrac{2}{\sqrt{b+2}+\sqrt{b}}\)
mà a>b>0
nên \(\sqrt{a+2}-\sqrt{a}< \sqrt{b+2}-\sqrt{b}\)
Đúng 1
Bình luận (0)
Cho a > b, hãy so sánh:
a) − 3 a + 4 và − 3 b + 4 b) 2 − 3 a và 2 − 3 b
Sử dụng mối liên hệ giữa thứ tự và phép nhân, phép cộng, chúng ta thu được
a) -3a + 4 < -3b + 4; b) 2 - 3a < 2 - 3b.
Đúng 0
Bình luận (0)
Cho a < b, hãy so sánh :
a) a + 1 và b + 1
b) a - 2 và b - 2
a) Ta có: a < b => a + 1 < b + 1
b) Ta có: a < b => a - 2 < b - 2
Đúng 0
Bình luận (0)
a) Ta có: a < b => a + 1 < b + 1
b) Ta có: a < b => a - 2 < b - 2
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho A =4+2^2+2^3+2^4 +...+2^99 và B =4^100 .Hãy so sánh A và B .
\(A=4+2^2+2^3+...+2^{99}\)
=> \(2A=8+2^3+2^4+...+2^{100}\)
=> \(2A-A=\left(8+2^3+2^4+...+2^{100}\right)-\left(4+2^2+2^3+...+2^{99}\right)\)
=> \(A=2^{100}< 2^{200}=2^{2.100}=4^{100}=B\)
Vậy A < B
Đúng 0
Bình luận (0)
Cho a < b , hãy so sánh :
a) a + 1 và b + 1
b) a - 2 và b - 2
Ta có
a ) a < b ↔ a + 1 < b + 1
b ) a <b ↔ a - 2 < b - 2
Đúng 0
Bình luận (0)
Love Học 24 = Trần Việt Hà = tự hỏi tự trả lời
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
a) Cho a, b , n thuộc Z và b > 0, n > 0
hãy so sánh hai số hữu tỉ a/b và a+n/b+n
Áp dụng kết quả trên hãy so sánh 2/7 và 4/9; -17/25 và -14/28; -31/19 và -21/29.
Cho hai biểu thức A=2+2^2+2^3+...+2^2004+2^2005 và B=2^20060-2
Hãy so sánh A và B