Cho hàm số y = 2 − x 2 . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số. Khi đó M − 2 m bằng
A. 0
B. 2 2
C. − 2
D. 2
Cho hàm số f ( x ) = x 3 - 3 x . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=|f(sinx+1)+2|. Giá trị biểu thức M + m bằng
A. 4.
B. 6.
C. 2.
D. 8.
Cho hàm số y = 2 - x 2 . Gọi M và n lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số. Khi đó M - 2 m bằng
A. 2 2
B. 0
C. - 2
D. 2
Cho hàm số y = 2 - x 2 Gọi M và n lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số. Khi đó
M - 2m bằng
A. 2 2
B. 0
C. - 2
D. 2
Đáp án D
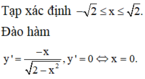
Bảng biến thiên:

Từ bảng biến thiên suy ra:
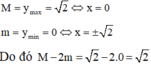
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2. sin x trên
đoạn - π 6 , 5 π 6 . Tính M, m.
A. M= 1, m = -1
B. M = 2, m = -2
C. M =1, m = -2
D. M = 2, m = -1
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2 . sin 2 x - cos x + 1 . Giá trị M + m bằng:
A. 0
B. 2
C. 25/8
D. 41/8
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2 − cosx . Tính M − m .
A. 2
B. -1
C. 1
D. 0
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y= x 2 + x + 3 x - 2 trên [-2;1] . Tính T=M+2m .
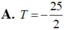
![]()
![]()
![]()
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2 − s i n x . Khẳng định nào dưới đây là đúng?
A. M = 1 ; m = − 1.
B. M = 2 ; m = 1.
C. M = 3 ; m = 0.
D. M = 3 ; m = 1.
Đáp án D.
Phương pháp
Sử dụng tập giá trị của hàm y = sin x : 1 ≤ sin x ≤ 1 để đánh giá hàm số bài cho
Cách giải
Ta có:
− 1 ≤ s i n x ≤ 1 ⇒ − 1 ≤ − s i n x ≤ 1
2 − 1 ≤ 2 − s i n x ≤ 2 + 1 ⇔ 1 ≤ 2 − s i n x ≤ 3 ⇒ M = 3 ; m = 1
Gọi M và N lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = - 1 + 2 . cos x 2 - 3 . sin x + cos x trên ℝ . Biểu thức M + N + 2 có giá trị bằng:
A. 0
B. 4 2 - 3
C. 2
D . 2 + 3 + 2